不动点与均衡（I）¶

作为博弈论进阶的开篇，我们希望探讨一系列不动点定理及其与均衡之间的关联——这无疑是一个令人着迷于其美感的话题。在泛函分析相关章节中，我们已经介绍了最基础的巴拿赫不动点定理及其应用，因此本讲我们从布劳威尔（Brouwer）不动点定理开始，也将介绍角谷（Kakutani）不动点定理和 KKM 定理，以及它们在纳什均衡存在性等方面的应用。

对于这一话题感兴趣的读者可以进一步翻阅 Fixed Point Theorems with Applications to Economics and Game Theory (Kim C. Border) 等相关教材。对于数理经济学感兴趣的可以参考《经济动态的递归方法》（Nancy L. Stokey，Robert E. Lucas），其中介绍了经济学相关的大量数学基础。

斯佩纳引理¶

为了介绍接下来的不动点定理，我们首先介绍斯佩纳（Sperner）引理。这里的介绍需要一些简单的单纯形的预修知识，可以参见凸优化基础知识，我们将紧接着其中的末尾部分继续我们的讨论。

着色的定义¶

回忆若 \(S = \langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\) 是 \(\mathbb{R}^n\) 中的一个单纯形，那么每个向量 \(y \in S\) 都可以唯一表示为 \(x^0,x^1,\cdots,x^k\) 的凸组合：\(y = \sum\limits_{l=0}^k \alpha^l x^l\)，其中 \(\alpha^l \geqslant 0\) 且 \(\sum\limits_{l=0}^k \alpha^l = 1\)。在此基础上，我们定义

\[\text{supp}_S(y) = \{ l \mid \alpha^l > 0 \}\]

为 \(y\) 的支撑集。回忆一下，如果 \(\mathcal{T}\) 是 \(S\) 的划分，那么 \(Y(\mathcal{T})\) 是 \(\mathcal{T}\) 内所有单纯形的极端点的集合，我们有如下定义：

单纯形划分的染色

令 \(S = \langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\) 是 \(\mathbb{R}^n\) 中的一个 \(k\) 维单纯形，对于 \(n \geqslant k\)，令 \(\mathcal{T}\) 是 \(S\) 的一个划分。\(\mathcal{T}\) 的一个着色（coloring）是一个从 \(Y(\mathcal{T})\) 到 \(\{0,1,\cdots,k\}\) 的映射 \(c\)，将每个极端点映射到一个颜色（每个颜色是一个指数）。如果对每个 \(y \in Y(\mathcal{T})\)，\(y\) 的颜色 \(c(y)\) 是 \(y\) 的支撑集中的某个指数，那么我们称这个着色是合适的（proper）。

这个定义说起来有些拗口，我们以三角形为例进行理解。三角形事实上是单纯形 \(S = \langle \langle x^0,x^1,x^2 \rangle \rangle\)，根据合适着色的要求，\(x^0\) 的支撑是 \(\{0\}\)，\(x^1\) 的支撑是 \(\{1\}\)，\(x^2\) 的支撑是 \(\{2\}\)，因此合适的着色是将 \(x^0\) 着色为 \(0\)，\(x^1\) 着色为 \(1\)，\(x^2\) 着色为 \(2\)。除此之外，位于 \(x^0\) 和 \(x^1\) 之间的点 \(x^3\) 的支撑是 \(\{0,1\}\)，因此它的着色可以是 \(0\) 或 \(1\)，但不能是 \(2\)，其余同理；而位于三角形内部的点的支撑是 \(\{0,1,2\}\)，因此它的着色可以是 \(0,1,2\) 中的任意一个。我们给出一个例子：

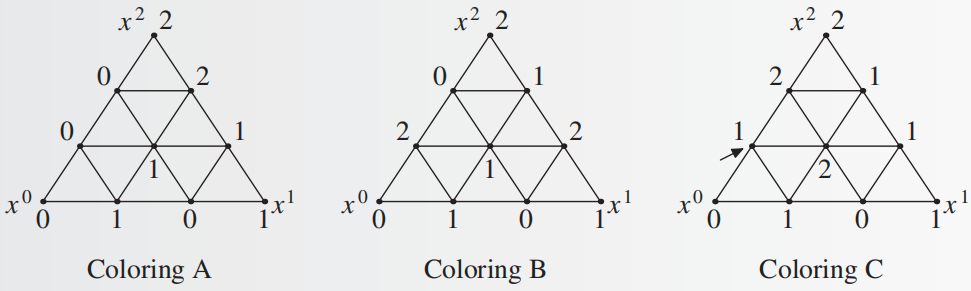
图中的 \(\text{A}\) 和 \(\text{B}\) 都是合适的着色，但 \(\text{C}\) 不是，因为箭头指向的点着色了 \(1\)，但这个点的支撑 \(x^0\) 和 \(x^2\) 的着色分别是 \(0\) 和 \(2\)。进一步地，我们可以定义完美着色的概念：

完美着色

令 \(\mathcal{T}\) 是 \(k\) 维单纯形 \(S\) 的划分，令 \(c\) 是 \(\mathcal{T}\) 的合适着色。\(k\) 维单纯形 \(T \in \mathcal{T}\) 是完美着色的（perfectly colored），如果 \(T\) 的 \(k+1\) 个极端点被 \(k+1\) 种不同的颜色着色。

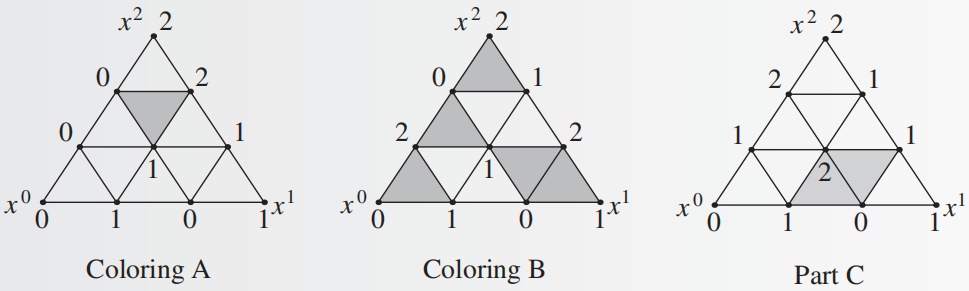
上图中每种着色中，完美着色的 \(k\) 维单纯形都被填充了灰色，我们发现合适的着色 \(\text{A}\) 和 \(\text{B}\) 中完美着色的 \(k\) 维单纯形有奇数个，而 \(\text{C}\) 表明不合适的着色中完美着色的 \(k\) 维单纯形可能出现偶数个。推广之后就是斯佩纳引理的内容：

斯佩纳引理

令 \(S\) 是 \(\mathbb{R}^n\) 中的一个 \(k\) 维单纯形，对于 \(n \geqslant k\)，令 \(\mathcal{T}\) 是 \(S\) 的一个划分。如果 \(c\) 是 \(\mathcal{T}\) 的一个合适着色，那么完美着色 \(k\) 维单纯形 \(T \in \mathcal{T}\) 的个数是奇数。特别地，\(\mathcal{T}\) 中至少有一个完美着色的 \(k\) 维单纯形。

斯佩纳引理的证明¶

斯佩纳引理的证明

根据单纯形的维数 \(k\) 使用数学归纳法：

第一步：\(k = 0\) 的情况

此时单纯形只包含一个点，显然引理成立。

第二步：\(k > 0\) 时，定义三类单纯形的集合

考虑 \(k > 0\) 的情况，假定定理陈述对每个 \(k - 1\) 维单纯形都成立，令 \(S = \langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\) 是一个 \(k\) 维单纯形，\(\mathcal{T}\) 是 \(S\) 的一个划分，\(c\) 是 \(\mathcal{T}\) 的一个合适着色。我们定义如下三类单纯形集合：

\(\mathcal{A}\) 表示 \(\mathcal{T}\) 中所有的被包含在 \(S\) 的边界内并被 \(\{0,1,\cdots,k-1\}\) 着色的 \(k-1\) 维单纯形；
\(\mathcal{B}\) 表示 \(\mathcal{T}\) 中所有被 \(\{0,1,\cdots,k-1\}\) 着色的 \(k\) 维单纯形，也就是说有两个节点被相同的颜色着色；
\(\mathcal{C}\) 表示 \(\mathcal{T}\) 中所有被 \(\{0,1,\cdots,k\}\) 着色的 \(k\) 维单纯形。

定义这几类单纯形集合的作用在之后就会看到，在那时回过头来看，这里的定义是非常巧妙的。我们来看一个例子：

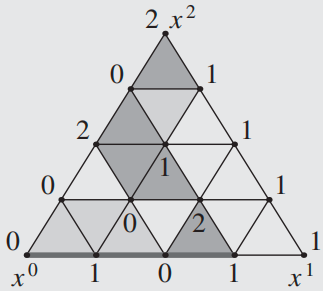
在上图中，\(\mathcal{A}\) 是三角形边界上被 \(\{0,1\}\) 染色的线段，被加粗表示；\(\mathcal{B}\) 是被 \(\{0,1\}\) 染色的小三角形，用浅色阴影表示；\(\mathcal{C}\) 是被 \(\{0,1,2\}\) 染色的小三角形，用深色阴影表示。我们可以看到，\(\mathcal{A}\) 中的线段有 \(3\) 个，\(\mathcal{B}\) 中的小三角形有 \(4\) 个，\(\mathcal{C}\) 中的小三角形有 \(5\) 个。

第三步：证明 \(\mathcal{A}\) 中的线段数是奇数

由于 \(\mathcal{A}\) 中的线段是 \(k-1\) 维单纯形，且被 \(\{0,1,\cdots,k-1\}\) 着色，根据归纳假设，\(\mathcal{A}\) 中的线段数是奇数。

第四步：构建连接单纯形之间的图

接下来我们定义无向图如下：

节点集为 \(\mathcal{A} \cup \mathcal{B} \cup \mathcal{C}\)，即 \(\mathcal{A} \cup \mathcal{B} \cup \mathcal{C}\) 中的每个单纯形都是图上的一个节点；
令 \(T_1,T_2\) 是 \(\mathcal{A} \cup \mathcal{B} \cup \mathcal{C}\) 中两个不同的单纯形，当且仅当 \(T_1 \cap T_2\) 是由 \(\{0,1,\cdots,k-1\}\) 着色的 \(k-1\) 维单纯形时，\(T_1\) 和 \(T_2\) 之间有一条边。

下图给出了一个如此定义的无向图的实例，其中短线就代表着单纯形之间的边：

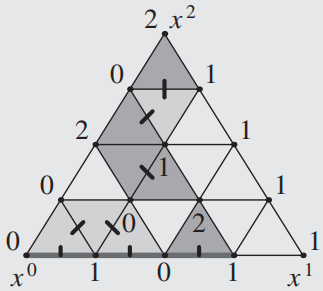
第五步：分析图的性质，得到最终结论

最后我们分析这个图中从 \(\mathcal{A},\mathcal{B},\mathcal{C}\) 出发的边数，从而得出结论：

从 \(\mathcal{A}\) 中每个节点出发，到 \(\mathcal{B}\) 或 \(\mathcal{C}\) 的边有且仅有一条：回忆凸优化基础知识的最后一个定理，\(\mathcal{A}\) 中每个节点根据定义都在边界上，因此只能在唯一的 \(k\) 维单纯形中；因为 \(\mathcal{A}\) 中每个节点已经有 \(k-1\) 个颜色，因此 \(\mathcal{A}\) 中每个节点所在的 \(k\) 维单纯形一定包含于 \(\mathcal{B}\) 或 \(\mathcal{C}\) 中，因此相连的边有且仅有一条；
从 \(\mathcal{B}\) 中每个节点出发，到 \(\mathcal{A}\) 或 \(\mathcal{C}\) 的边有且仅有两条：因为 \(\mathcal{B}\) 中的每个节点都被 \(\{0,1,\cdots,k-1\}\) 着色，因此有且仅有两个 \(k-1\) 维子单纯形（或者说面）被 \(\{0,1,\cdots,k-1\}\) 着色（因为有一种颜色被两个极端点使用，其余颜色都是一一对应）
- 如果这样的 \(k-1\) 维单纯形在边界上，那么符合 \(\mathcal{A}\) 和 \(\mathcal{B}\) 相连的条件，因此有一条边；
- 如果这样的 \(k-1\) 维单纯形在内部，回忆凸优化基础知识的最后一个定理，这样的单纯形包含于两个 \(k\) 维单纯形，并且因为这个 \(k-1\) 维单纯形已经使用了 \(\{0,1,\cdots,k-1\}\)，因此这两个 \(k\) 维单纯形一个在 \(\mathcal{B}\) 中（因为现在探讨的是 \(\mathcal{B}\) 中每个节点出发的情况），令一个在 \(\mathcal{B}\) 或 \(\mathcal{C}\) 中，也是有一条边连接的；
- 因此这样的 \(k-1\) 维单纯形无论如何都会带来一条边的连接，而我们有两个这样的单纯形，因此有两条边；
从 \(\mathcal{C}\) 中每个节点出发，到 \(\mathcal{A}\) 或 \(\mathcal{B}\) 的边有且仅有一条：因为 \(\mathcal{C}\) 中的每个节点都被 \(\{0,1,\cdots,k\}\) 着色，因此有且仅有一个 \(k-1\) 维子单纯形被 \(\{0,1,\cdots,k-1\}\) 着色（因为此时点和颜色一一对应），根据和 \(\mathcal{B}\) 类似的讨论即可得到结论。

事实上，从图中所有节点出发的边的总数，等于边的数量 \(R\) 的两倍，因为每条边都被数了两次，这意味着

\[2R = |\mathcal{A}| + 2|\mathcal{B}| + |\mathcal{C}|\]

因此等号右边是偶数，而 \(|\mathcal{A}|\) 是奇数，因此 \(|\mathcal{C}|\) 也是奇数，注意 \(\mathcal{C}\) 的定义就是完美着色的 \(k\) 维单纯形的集合，因此斯佩纳引理得证。

不得不承认的一点是，这个证明的整体过程看完有一种不知道怎么就证出来的感觉，事实上回过头来体会就会发现其中的构造都非常的精妙，整体而言就是分了三类单纯形，构造了一种特殊的图，第一类数量可以用归纳假设，第二类图中产生边数为偶数，第三类是目标，数量根据奇偶性分析直接可以得到，或许这就是奇妙的组合学吧！

单纯形划分的进一步性质¶

接下来的内容将会在之后的证明中用到，因此做一个简单的介绍：

单纯形与单纯形划分的直径

令 \(S = \langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\) 是 \(\mathbb{R}^n\) 中的一个 \(k\) 维单纯形，对于 \(n \geqslant k\)，令 \(\mathcal{T} = \{T_1,T_2,\cdots,T_M\}\) 是 \(S\) 的一个划分。\(S\) 的直径（diameter）定义为

\[\rho(S) = \max\limits_{i,j} \| x^i - x^j \|\]

其中 \(i,j\) 遍历 \(0,1,\cdots,k\)。也就是说，单纯形的直径是最远的极端点之间的距离，事实上这也是单纯形内任意两点的最大距离，事实上只需要注意到单纯形是凸集就并不难理解。进一步地，\(\mathcal{T}\) 的直径（diameter）定义为

\[\rho(\mathcal{T}) = \max\limits_{m=1,2,\cdots,M} \rho(T_m)\]

也就是说，单纯形划分的直径是划分中最大的单纯形的直径。

下面的定理表明，每个单纯形划分都可以“加细”，或者说被精炼为具有更小直径的划分：

单纯形划分的精炼

令 \(k \geqslant 1\)，\(\mathcal{T}\) 是 \(\mathbb{R}^n\) 中的一个 \(k\) 维单纯形 \(S = \langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\) 的一个划分。那么存在 \(S\) 的一个划分 \(\mathcal{T'}\)，满足如下要求：

对每个 \(T' \in \mathcal{T'}\)，都存在 \(T \in \mathcal{T}\)，使得 \(T \subseteq T'\)；
\(\rho(\mathcal{T'}) \leqslant \dfrac{k}{k+1} \rho(\mathcal{T})\)。

反复运用上述定理即可得到如下推论，之后我们会默认熟知这一结果推导其他结果：

单纯形划分精炼的推论

对每个单纯形 \(S\) 和任意的 \(\varepsilon > 0\)，存在一个划分 \(\mathcal{T_\varepsilon}\)，使得 \(\rho(\mathcal{T_\varepsilon}) < \varepsilon\)。

定理的证明技术性较强，暂时略去（或许一直都会略去了）。证明方式就是构造出符合条件的划分精炼，如果读者对证明感兴趣可以参考我们的一本参考资料：《博弈论》[以] 迈克尔·马希勒，埃隆·索兰，什穆埃尔·扎米尔。

布劳威尔不动点定理¶

定理陈述与证明¶

我们已经做了充足的准备来迎接本节的第一个核心定理：布劳威尔（Brouwer）不动点定理。这个定理是拓扑学中的一个基本定理，事实上有非常多种证明方式，大多数都需要利用拓扑学知识，因此我们只能选取一条技术性更强的路线，即使用前面介绍的斯佩纳引理来证明。我们首先给出定理的陈述，然后逐步展开我们的讨论，直至完全证明这一定理：

布劳威尔不动点定理

令 \(X\) 是 \(\mathbb{R}^n\) 中的一个非空闭凸集，\(f: X \to X\) 是一个连续映射，那么 \(f\) 至少有一个不动点，即存在 \(x \in X\)，使得 \(f(x) = x\)。

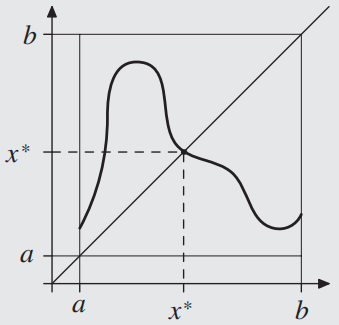
上图给出了定理在 \(n=1\) 的情况下的例子，显然 \([a,b] \to [a,b]\) 的连续映射无论怎么画都会和 \(i(x)= x\) 相交。对于二维的情况，一个例子是如果你把世界地图平铺在地面上，那么一定存在地面上的一个点，与其上方地图上的一个点代表同一位置。或者更生活化地，大商场等地方可以看到的平面地图，上面标有“您在此处”的红点。如果标注足够精确，那么这个点就是把实际地形射到地图的连续函数的不动点。

为了证明这一定理的一般情况，我们首先证明一个特殊情况，即 \(X\) 是标准单纯形（standard simplex）的情况。\(n-1\) 维标准单纯形 \(X(n)\) 定义如下：

\[X(n) = \{ x \in \mathbb{R}^n \mid x_i \geqslant 0, \sum\limits_{i=1}^n x_i = 1 \}\]

下图给出了三个最简单的标准单纯形，不能看出 \(n-1\) 维标准单纯形就是顶点为 \(e_1,\cdots,e_n\)（自然基）的单纯形。

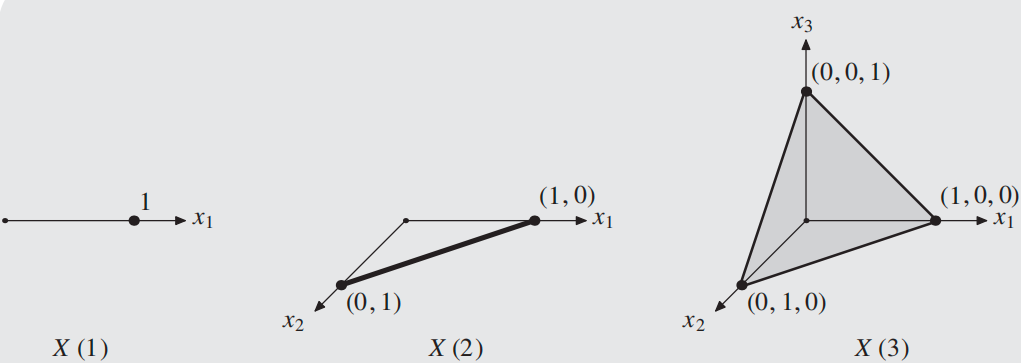
我们首先证明如下特殊情况：

布劳威尔不动点定理的特殊情况

令 \(f: X(n) \to X(n)\) 是一个连续映射，那么 \(f\) 至少有一个不动点。

在定理的证明中，我们需要用到 \(\mathbb{R}^n\) 的上范数（sup-norm）：对于 \(x = (x_1,x_2,\cdots,x_n) \in \mathbb{R}^n\)，定义

\[\| x \|_\infty = \max\limits_{i=1,2,\cdots,n} |x_i|\]

布劳威尔不动点定理的特殊情况证明

对任意的 \(y \in X(n)\)，都有 \(y = \sum\limits_{i=1}^n y_i e_i\)，其中 \(e_i\) 是 \(\mathbb{R}^n\) 的自然基。于是 \(y\) 的支撑 \(\text{supp}_{X(n)}(y)\) 是 \(\{ i \mid y_i > 0 \}\)。

第一步：对每个 \(y \in X(n)\)，存在 \(i \in \text{supp}_{X(n)}(y)\) 满足 \(f_i(y) \leqslant y_i\)

根据 \(f: X(n) \to X(n)\) 可知 \(\sum\limits_{i=1}^n y_i = \sum\limits_{i=1}^n f_i(y) = 1\) 且 \(f(y_i) \geqslant 0\)，反证法，假设对每个 \(i \in \text{supp}_{X(n)}(y)\) 都有 \(f_i(y) > y_i\)，而我们知道对每个 \(i \notin \text{supp}_{X(n)}(y)\)，\(f_i(y) \geqslant 0 = y_i\)，因此此时有 \(\sum\limits_{i=1}^n f_i(y) > \sum\limits_{i=1}^n y_i = 1\)，与 \(f\) 是 \(X(n)\) 到 \(X(n)\) 的映射矛盾。

第二步：定义一个着色

因为紧集上的连续函数都是一致连续的，因此对于任意的 \(\varepsilon > 0\)，存在 \(\delta > 0\)，使得对于任意的 \(x,y \in X(n)\)，只要 \(\| x - y \|_\infty < \delta\)，就有 \(\| f(x) - f(y) \|_\infty < \varepsilon\)。从而我们定义 \(X(n)\) 的划分 \(\mathcal{T}_\varepsilon\)，使得对于任意的 \(T_\varepsilon \in \mathcal{T}_\varepsilon\)，\(\rho(T_\varepsilon) < \delta\)。为了之后讨论的方便，这里的 \(\delta\) 我们都取小于等于 \(\epsilon\) 的值。

我们定义一个着色 \(c\)，使得对每个 \(x \in Y(\mathcal{T}_\varepsilon)\)，\(c(x) = i\) 当且仅当 \(i \in \text{supp}_{X(n)}(y)\) 且 \(f_i(x) \leqslant x_i\)。根据第一步的讨论，这样的 \(i\) 一定存在，并且这个着色是合适的，因为 \(c(x)\) 取的是 \(x\) 的支撑集中的某个指数。根据斯佩纳引理，我们知道至少有一个完美着色的 \(n-1\) 维单纯形 \(T_\varepsilon \in \mathcal{T}_\varepsilon\)。

第三步：不动点的存在性

我们设这个完美着色的单纯形为 \(T_\varepsilon = \langle \langle x^1,x^2,\cdots,x^n \rangle \rangle\)，其所有节点被 \(\{1,2,\cdots,n\}\) 着色，不妨设 \(c(x^i) = i\)，即 \(f_i(x^i) \leqslant x_i^i\) 成立（\(x_i^i\) 是 \(x^i\) 的第 \(i\) 个坐标）。令 \(x^\varepsilon\) 是 \(T_\varepsilon\) 中的一个向量，因为 \(\rho(T_\varepsilon) < \delta\)，这意味着 \(\| x^\varepsilon - x^i \|_\infty < \delta\) 对每个 \(i\) 都成立，因此根据 \(f\) 的一致连续性，有

\[f_i(x^\varepsilon) \leqslant f_i(x^i) + \varepsilon \leqslant x_i^i + \varepsilon \leqslant x_i^\varepsilon + \varepsilon + \delta \leqslant x_i^\varepsilon + 2\varepsilon, \forall i \in [n]\]

上式对于任意的 \(\varepsilon\) 都成立，因此存在点列 \((x^\varepsilon)_{\varepsilon > 0}\)，使得

\[\begin{equation} f_i(x^\varepsilon) \leqslant x_i^\varepsilon + 2\varepsilon \tag{1} \label{brouwer} \end{equation}\]

对每个 \(i\) 都成立。根据 \(X(n)\) 的紧性，存在一个收敛的子列 \((x^{\varepsilon_k})_{k=1}^\infty\)，收敛到一个点 \(x^* \in X(n)\)。根据 \(f\) 的连续性，对 \(\eqref{brouwer}\) 取极限，有 \(f_i(x^*) \leqslant x_i^*,\forall i \in [n]\)，而回忆 \(\sum\limits_{i=1}^n x_i^* = \sum\limits_{i=1}^n f_i(x^*) = 1\)，因此有 \(f_i(x^*) = x_i^*,\forall i \in [n]\)，从而 \(f(x^*) = x^*\)，即 \(f\) 至少有一个不动点。

事实上，任何一个 \(k\) 维单纯形 \(S\) 都等价于标准单纯形 \(X(k+1)\)（只需要将顶点一一对应后，使用重心坐标即可，不影响我们上面的证明），所以这一定理对任意的单纯形也都是成立的。总结一下上述证明，核心在于构造了一个合适的着色，然后利用斯佩纳引理得到了一个完美着色的单纯形，最后通过一致连续性和紧性得到了不动点的存在性，事实上最终的不动点就是一个极限点。

接下来我们需要将布劳威尔不动点定理推广到一般的凸紧集的情况，我们需要首先证明如下引理：

引理

令 \(X\) 是 \(\mathbb{R}^n\) 中的一个非空凸紧集，定义函数 \(g: \mathbb{R}^n \to X\)，使得 \(g(x)\) 是 \(X\) 中距离 \(x\) 最近的点。那么 \(d(g(x),g(y)) \leqslant d(x,y), \forall x,y \in \mathbb{R}^n\)。

回忆对于闭凸集 \(X\) 而言，对于 \(x \notin X\)，存在唯一的 \(y \in X\)，使得 \(d(x,y) = d(x,X)\)，这个 \(y\) 就是 \(g(x)\)，即 \(g\) 是良定义的。这一引理表明，\(g\) 是一个 Lipschitz 连续的映射，因此也是连续的。

引理的证明

回忆凸优化基础知识中关于分离超平面定理的证明，对于 \(x \notin X\)，设 \(y\) 是 \(X\) 中距离 \(x\) 最近的点，\(z\) 是 \(X\) 中任一点，则有 \(\langle x-y,z-y \rangle \leqslant 0\)。代入引理的符号，有 \(\langle x-g(x),g(y)-g(x) \rangle \leqslant 0\)，同理有 \(\langle y-g(y),g(x)-g(y) \rangle \leqslant 0\)，两式相加得到

\[\langle (g(y) - g(x)) - (y-x),g(y)-g(x) \rangle \leqslant 0\]

在做好一切准备工作后，我们就可以开始证明最终的定理了：

布劳威尔不动点定理的证明

因为 \(X\) 是紧集，因此存在一个足够大的单纯形 \(S\) 包含 \(X\)。定义函数 \(h: S \to S\) 满足 \(h(x) = f(g(x))\)，其中 \(g\) 是引理中定义的函数。根据引理，\(g\) 是连续函数，又 \(f\) 也是连续函数，因此 \(h\) 是连续的，因此根据特殊情况的证明，\(h\) 至少有一个不动点 \(x^* \in S\)，即 \(f(g(x^*)) = h(x^*) = x^*\)。注意到函数 \(h\) 的实际值域是 \(f\) 的值域，因此包含于 \(X\)，因此 \(x^* \in X\)，因此根据定义 \(g(x^*) = x^*\)，因此 \(f(x^*) = x^*\)，即 \(f\) 至少有一个不动点。

布劳威尔不动点定理相关的历史

布劳威尔不动点定理是代数拓扑的早期成就，还是更多更一般的不动点定理的基础，在泛函分析中尤其重要。在 1904 年，首先由 Piers Bohl 证明 \(n = 3\) 的情况。后来在 1909 年，鲁伊兹·布劳威尔（L. E. J. Brouwer）再次证明。在1910年，雅克·阿达马提供一般情况的证明，而布劳威尔在 1912 年提出另一个不同的证明。这些早期的证明皆属于非构造性的间接证明，与数学直觉主义理想矛盾。直到 1967 年，美国数学家 H. E. Scarf 找到了计算单纯形连续映射不动点的组合拓扑有限算法，这也就是 Brouwer 不动点定理的构造性证明。我们从斯佩纳引理出发的证明来源于 Kuhn（1960）。

布劳威尔不动点定理在无限维空间中的推广是邵德尔（Schauder）不动点定理，即每一个从一个巴拿赫空间的某个给定的凸紧子集射到它自身的连续函数都有（至少）一个不动点。

布劳威尔不动点定理的推广

我们考虑一个简单的推广：\(f: X \to X\) 中的 \(X\) 不再强制要求是凸紧集，可以只是一个同胚于一个凸紧集的紧集。那么布劳威尔不动点定理是否仍然成立呢？

答案是成立的，设 \(g: X \to S\) 是同胚映射，其中 \(S\) 是凸紧集，构造 \(h: S \to S\) 满足 \(h(x) = g(f(g^{-1}(x)))\)，根据同胚的要求以及布劳威尔不动点定理，\(h\) 存在不动点 \(x^* \in S\)，即 \(g(f(g^{-1}(x^*))) = x^*\)，因此 \(f(g^{-1}(x^*)) = g^{-1}(x^*)\)，、因此 \(f\) 至少有一个不动点 \(g^{-1}(x^*)\)。

定理的应用¶

接下来我们将应用布劳威尔不动点定理证明纳什定理：

纳什定理

对于任意一个策略式博弈 \(G = (N,(S_i)_{i\in N},(u_i)_{i\in N})\)，如果参与人的个数有限，每个参与人的策略集是有限的，那么必然存在一个混合策略纳什均衡。

我们假设 \(G\) 的混合扩展为 \(\Gamma = (N,(\Sigma_i)_{i\in N},(U_i)_{i\in N})\)，并且 \(|S_i| = m_i\)。为了我们接下来的证明，我们不加说明地给出两个很简单的结论：

纳什定理的引理

如果参与人 \(i\) 的纯策略集是有限的，那么参与人 \(i\) 的混合策略集 \(\Sigma_i\) 是凸紧的（事实上是单纯形，极端点是所有可能的纯策略向量）；
如果 \(A \subset \mathbb{R}^n\) 和 \(B \subset \mathbb{R}^m\) 都是凸（紧）集，那么 \(A \times B \subset \mathbb{R}^{n+m}\) 也是凸（紧）的。

综合引理的两个结论可知，集合 \(\Sigma = \Sigma_1 \times \Sigma_2 \times \cdots \times \Sigma_n\) 是凸紧的，因此接下来我们的整体思路是：构造 \(f: \Sigma \to \Sigma\)，使得 \(f\) 是一个连续映射，然后根据布劳威尔不动点定理，证明 \(f\) 至少有一个不动点，并且这个不动点恰好是一个混合策略纳什均衡。

定理的正式证明我们逐步分析得到，因为这里 \(f\) 的构造需要逐步分析才更好理解背后的含义。事实上，因为 \(f: \Sigma \to \Sigma\)，所以 \(f\) 将一个混合策略映射到另一个混合策略。如果 \(\sigma\) 不是混合策略纳什均衡，那么存在一个参与人 \(i\)，\(\sigma_i\) 不是 \(\sigma_{-i}\) 的最佳应对，故我们令 \(f_i(\sigma)\) 为参与人 \(i\) 比 \(\sigma_i\) 更优的对 \(\sigma_{-i}\) 的应对，即一个向着均衡方向的改进。这样的定义思想使得，\(\sigma\) 是混合策略纳什均衡当且仅当 \(f(\sigma) = \sigma\)，因为此时每个人都已经处于最优应对了。

以上只是一些想法，要真的定义出这个 \(f\)，我们首先需要一个辅助函数 \(g_i^j: \Sigma \to [0,+\infty)\)，满足

\[g_i^j(\sigma) = \max\{0, U_i(s_i^j,\sigma_{-i}) - U_i(\sigma)\}\]

也就是说，\(g_i^j\) 是参与人 \(i\) 从 \(\sigma_i\) 转向纯策略 \(s_i^j\) 带来的收益。如果收益大于零则为收益，否则为零。一个很显然的结论是，当且仅当 \(\forall i,j\) 都有 \(g_i^j(\sigma) = 0\) 时，\(\sigma\) 是混合策略纳什均衡，因为纳什均衡是最优反应。

现在我们可以定义 \(f\)，使其符合我们之前讨论的直观：当 \(\sigma\) 不是均衡时，\(f_i(\sigma)\) 能转向更优反应。因为 \(f(\sigma)\) 仍然是混合策略向量，故记 \(f_i^j(\sigma)\) 为取值 \(\sigma\) 时，参与人 \(i\) 选择纯策略 \(s_i^j\) 的概率。事实上如果 \(\sigma_i\) 不是 \(\sigma_{-i}\) 的最优应对，那么我们应当将 \(i\) 选择更优的纯策略的概率增大，因此我们可以令

\[f_i^j(\sigma) = \dfrac{\sigma_i(s_i^j)+g_i^j(\sigma)}{1+\sum\limits_{k=1}^{m_i} g_i^k(\sigma)}\]

这非常符合我们的直观，并且分母上的值也使得 \(\sum\limits_{j=1}^{m_i} f_i^j(\sigma) = 1\)，即 \(f_i(\sigma)\) 仍然是一个混合策略，即的确满足 \(f: \Sigma \to \Sigma\)。除此之外，我们知道 \(U_i\) 都是连续函数（因为是多重线性函数），\(g\) 是两个连续函数的最大值，因此也是连续函数，而 \(f\) 的分母一定大于 \(0\)，因此 \(f\) 也是连续函数，根据布劳威尔不动点定理，\(f\) 至少有一个不动点，即存在 \(\sigma^* \in \Sigma\)，使得 \(f(\sigma^*) = \sigma^*\)，下面我们就要证明 \(\sigma^*\) 的确是一个混合策略纳什均衡。

\(\sigma^*\) 的确是一个混合策略纳什均衡

因为 \(\sigma^*\) 是一个不动点，因此 \(f(\sigma^*) = \sigma^*\)，即 \(f_i^j(\sigma^*) = \sigma_i^*(s_i^j) = \dfrac{\sigma_i^*(s_i^j)+g_i^j(\sigma^*)}{1+\sum\limits_{k=1}^{m_i} g_i^k(\sigma^*)}\)，整理得到

\[g_i^j(\sigma) = \sigma_i(s_i^j)\sum\limits_{k=1}^{m_i} g_i^k(\sigma),\forall i \in N, j \in [m_i]\]

使用反证法，假设这一不动点 \(\sigma^*\) 不是混合策略纳什均衡，那么必定存在一个参与人 \(i\) 以及 \(l \in [m_i]\) 使得 \(g_i^l(\sigma) > 0\)。特别地，\(\sum\limits_{k=1}^{m_i} g_i^k(\sigma) > 0\)，因此根据上式我们得到

\[\begin{equation} \sigma_i(s_i^j) > 0 \iff g_i^j(\sigma) > 0, \forall j \in [m_i] \tag{3} \label{nash-1} \end{equation}\]

因为 \(U_i\) 是多线性的，因此 \(U_i(\sigma) = \sum\limits_{j=1}^{m_i} \sigma_i(s_i^j) U_i(s_i^j,\sigma_{-i})\)，这意味着

\[\begin{align} 0 &= \sum\limits_{j=1}^{m_i} \sigma_i^*(s_i^j) (U_i(s_i^j,\sigma_{-i}) - U_i(\sigma^*)) \\ &= \sum\limits_{j: \sigma_i(s_i^j) > 0} \sigma_i^*(s_i^j) (U_i(s_i^j,\sigma_{-i}) - U_i(\sigma^*)) \\ &= \sum\limits_{j: \sigma_i(s_i^j) > 0} \sigma_i^*(s_i^j) g_i^j(\sigma) \\ \end{align}\]

然而我们知道\(g_i^l(\sigma) > 0\)，根据 \(\eqref{nash-1}\)，我们知道 \(\sigma_i^*(s_i^l) > 0\)，因此上式的和大于 \(0\)，这与 \(0\) 的等式矛盾，因此假设不成立，\(\sigma^*\) 是一个混合策略纳什均衡。

由此我们便证明了纳什均衡的存在性。事实上这一证明非常美丽，对 \(f\) 的构造也非常优雅美观，因此这一证明值得重视。接下来我们讨论纳什定理的一个拓展，因为有时候存在约束使得参与人 \(i\) 无法选择整个 \(\Sigma_i\)，例如要求选择某个纯策略的概率必须大于等于一个值。在这样的情况下，约束条件可以转化为线性不等式，而有限数目的半空间相交得到的有界集合称为多面体（polytope）。事实上多面体可以视为其极值点的凸包，只是这些极值点不一定仿射无关（这是单纯形的要求）了，例如四边形不是单纯形，但是是多面体。事实上，当参与人的策略空间是多面体时，纳什定理也成立：

纳什定理的一般化

令 \(\Gamma = (N,(X_i)_{i\in N},(U_i)_{i\in N})\) 是一个策略式博弈，对每个参与人 \(i\)，集合 \(X_i\) 是 \(\mathbb{R}^{d_i}\) 上的一个多面体，\(U_i\) 是多重线性函数，那么 \(\Gamma\) 至少有一个混合策略纳什均衡。

具体证明略去，事实上就是将多面体的极端点都视为纯策略，定义一个辅助的博弈即可。

角谷不动点定理¶

定理陈述与证明¶

角谷（Kakutani）不动点定理是由日本数学家角谷静夫提出的，它是布劳威尔不动点定理的一个推广，也是一个非常重要的不动点定理：在纳什本人的论文中，纳什定理的证明首先使用了布劳威尔不动点定理，之后的版本则在大卫·盖尔（David Gale）的建议下使用了更简单的角谷不动点定理。

3n + 1 猜想

事实上，提到角谷静夫，最令人熟知的可能是著名的 \(3n+1\) 猜想，即角谷猜想（事实上并不是他提出的，但因为他也对这一问题投入了研究所以也冠以他的名字），这个猜想是一个非常有趣且至今未被证明的数学问题，它的描述如下：对于每一个正整数，如果它是奇数，则对它乘 \(3\) 再加 \(1\)，如果它是偶数，则对它除以 \(2\)，如此循环，最终都能够得到 \(1\)。

为了描述角谷不动点定理，我们需要引入”半连续性“的概念，实际上是一般的连续性概念的推广：

半连续性

设 \(f(x)\) 定义在 \(X \subset \mathbb{R}^n\) 上，在 \(x_0\) 及其附近有定义，则

如果 \(\forall \varepsilon > 0\)，\(\exists \delta > 0\)，使得 \(\forall x \in X\)，只要 \(\| x - x_0 \| < \delta\)，就有 \(f(x) < f(x_0) + \varepsilon\)，则称 \(f(x)\) 在 \(x_0\) 处上半连续；
如果 \(\forall \varepsilon > 0\)，\(\exists \delta > 0\)，使得 \(\forall x \in X\)，只要 \(\| x - x_0 \| < \delta\)，就有 \(f(x_0) - \varepsilon < f(x)\)，则称 \(f(x)\) 在 \(x_0\) 处下半连续。

比较连续性的定义：\(\forall \varepsilon > 0\)，\(\exists \delta > 0\)，使得 \(\forall x \in X\)，只要 \(\| x - x_0 \| < \delta\)，就有 \(|f(x) - f(x_0)| < \varepsilon\)，我们知道函数在 \(x_0\) 处连续当且仅当它在 \(x_0\) 处既上半连续又下半连续。下图可以用来直观描述上、下半连续函数，其中左图是上半连续函数，右图是下半连续函数：

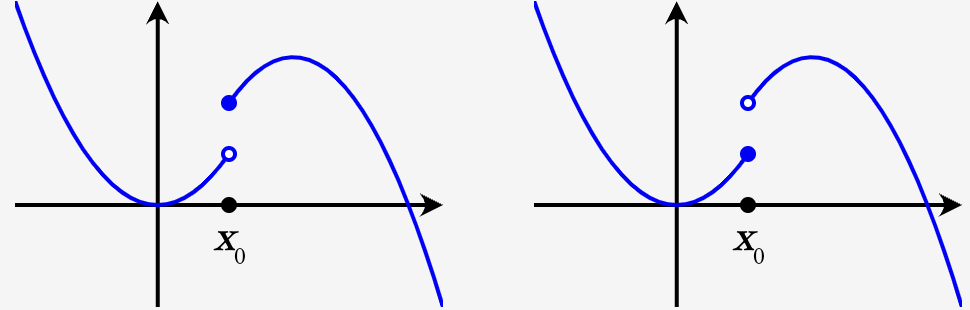
角谷不动点定理描述的是所谓的“集值函数”，即取值是集合的函数 \(F: X \to 2^X\)，其中 \(2^X\) 表示 \(X\) 的幂集。\(F\) 的图像指的是集合 \(\{(x,y) \in X \times X \mid y \in F(x)\}\)，实际上就是 \(F\) 在平面上的图像。基于此我们给出角谷不动点定理的陈述：

角谷不动点定理

令 \(X\) 是 \(\mathbb{R}^n\) 中的一个非空凸紧集，\(F: X \to 2^X\) 是一个上半连续的集值函数，满足对每个 \(x \in X\)，\(F(x)\) 是非空闭凸集，那么 \(F\) 至少有一个不动点，即存在 \(x^* \in X\)，使得 \(x^* \in F(x^*)\)。

集值函数的上半连续实际上就是 \(F\) 的图像是闭集，事实上集值函数的闭图像定理表明，对紧致的豪斯多夫空间 \(Y\)，一个集值函数 \({\displaystyle \varphi :X\to 2^{Y}}\)有闭图像的充分必要条件是：\(\varphi\) 是上半连续的，且对所有 \(x\)，\(\varphi(x)\) 是闭集。因为所有欧几里得空间都为豪斯多夫空间，故上述定理还可以重述为：

角谷不动点定理的另一表述

令 \(X\) 是 \(\mathbb{R}^n\) 中的一个非空凸紧集，\(F: X \to 2^X\) 一个集值函数，\(F\) 有闭图像且对每个 \(x \in X\)，\(F(x)\) 是非空凸集，那么 \(F\) 至少有一个不动点。

一些例子

有无穷多个不动点的函数

例如：函数 \({\displaystyle \varphi(x) = [1-x/2,1-x/4]}\) 满足所有角谷不动点定理的条件，并存在无穷多个不动点。

有一个不动点的函数

例如：一个函数 \({\displaystyle \varphi (x)={\begin{cases}3/4&0\leqslant x<0.5\\ [0,1]&x=0.5\\1/4&0.5<x\leqslant 1\end{cases}}}\) 满足所有角谷不动点定理的条件，存在唯一一个不动点 \({\displaystyle x=0.5}\)。

不满足凸集的函数

例如：一个函数 \({\displaystyle \varphi (x)={\begin{cases}3/4&0\leqslant x<0.5\\\{3/4,1/4\}&x=0.5\\1/4&0.5<x\leqslant 1\end{cases}}}\) 在 \({\displaystyle x=0.5}\) 处不满足凸集定义，但满足其他角谷不动点定理的条件。这个函数没有不动点。

不满足闭合图的函数

例如：一个函数 \({\displaystyle \varphi (x)={\begin{cases}3/4&0\leqslant x<0.5\\1/4&0.5\leqslant x\leqslant 1\end{cases}}}\) 不存在不动点，因为函数不满足闭图像。考虑序列 \({\displaystyle x_{n}=0.5-1/n}\) 和 \({\displaystyle y_{n}=3/4}\)：当 \({\displaystyle x_{n}\to x=0.5,y_{n}\to y=3/4,y\notin \varphi (x)}\)。

事实上角谷不动点定理是布劳威尔不动点定理的推广：取 \(F(x) = \{f(x)\}\)，那么角谷不动点定理就是布劳威尔不动点定理。为了证明角谷不动点定理，我们需要首先给出一些定义，然后证明一个引理。对 \(\mathbb{R}^n\) 中的每个子集 \(A\)，以及任意的 \(\varepsilon > 0\)，用 \(B(A,\varepsilon)\) 表示 \(A\) 的 \(\varepsilon\)-邻域，即 \(B(A,\varepsilon) = \{ x \in \mathbb{R}^n \mid d(x,A) < \varepsilon \}\)。

显然，如果 \(A\) 是凸集，那么 \(B(A,\varepsilon)\) 也是凸集。下面的引理说的是，对上半连续的集值函数 \(F\)，如果 \(x\) “接近于” \(x_0\)，那么 \(F(x)\) “接近于” \(F(x^0)\)：

引理

令 \(F: X \to 2^X\) 是上半连续集值函数（\(X\) 是紧集），对每个 \(x^0 \in X\) 和任意的 \(\varepsilon\)，都存在 \(\delta > 0\) 使得 \(F(x) \subseteq B(F(x^0),\varepsilon)\) 对所有满足 \(d(x,x^0) \leqslant \delta\) 的 \(x \in X\) 成立。

引理的证明

使用反证法：假设存在 \(x^0 \in X\) 和 \(\varepsilon\)，对任意的 \(\delta > 0\)，都存在 \(x^\delta \in X\) 满足 \(d(x^\delta,x^0) \leqslant \delta\)，存在 \(y^\delta \in F(x^\delta)\)，使得 \(d(y^\delta,F(x^0)) > \varepsilon\) 成立。因为 \(X\) 是紧集，可以取 \((x^\delta)\) 和 \((y^\delta)\) 的收敛子列 \((x^k)_{k \in \mathbb{N}}\) 和 \((y^k)_{k \in \mathbb{N}}\)，满足

\(\lim\limits_{k \to \infty} x^k = x^0\)，因为 \(\delta \to 0\)；
\(y^k \in F(x^k)\) 对每个 \(k \in \mathbb{N}\) 都成立，极限 \(\hat{y} = \lim\limits_{k \to \infty} y^k\) 存在；
\(d(y^k,F(x^0)) > \varepsilon\) 对每个 \(k \in \mathbb{N}\) 都成立。

根据 1、2 以及 \(F\) 的图像是闭集（因此 \((x_k,y_k)\) 的极限点仍然 \(F\) 的图像内）可知，\(\hat{y} \in F(x^0)\)，但是 \(d(\hat{y},F(x^0)) \geqslant \varepsilon\)，矛盾。

接下来我们可以开始证明角谷不动点定理，证明的大致思路是，构造一个 \(X \to X\) 的连续函数序列 \((f^m)_{m \in \mathbb{N}}\)，利用布劳威尔不动点定理，这个序列的每个函数都有一个不动点，然后证明这些不动点的极限点就是 \(F\) 的不动点。

角谷不动点定理的证明

第一步：定义连续函数的序列

对每个 \(m \in \mathbb{N}\)，定义 \(f^m: X \to X\)。因为 \(X\) 是紧集，故可以被有限个开球覆盖（假设 \(K^m\) 个），每个开球的半径为 \(\dfrac{1}{m}\)。用 \((x_k^m)_{k=1}^{K_m}\) 表示这些球的中心，那么对任意的 \(x \in X\)，都存在 \(k\) 使得 \(d(x,x_k^m) < \dfrac{1}{m}\)。对每个 \(k \in [K_m]\)，选择 \(y_k^m \in F(x_k^m)\)。用 \(C_k^m\) 表示与 \(x_k^m\) 距离至少为 \(\dfrac{1}{m}\) 的点集：

\[C_k^m = \{ x \in X \mid d(x,x_k^m) \geqslant \dfrac{1}{m} \}\]

这意味着 \(d(x,x_k^m) \leqslant \dfrac{1}{m}\) 当且仅当 \(x \notin C_k^m\)。因为 \(C_k^m\) 是闭集，这当且仅当 \(d(x,C_k^m) > 0\) 才能发生。对每个 \(x \in X\) 和每个 \(k \in [K_m]\)，定义

\[\lambda_k^m(x) = \dfrac{d(x,C_k^m)}{\sum\limits_{l=1}^{K_m} d(x,C_l^m)}\]

根据前面的讨论，分母一定是正数。而我们知道距离函数 \(x \mapsto d(x,C_k^m)\) 是连续的，因此 \(\lambda_k^m(x)\) 也是连续的。定义 \(f^m: X \to X\) 为

\[f^m(x) = \sum\limits_{k=1}^{K_m} \lambda_k^m(x) y_k^m\]

注意到 \(\sum\limits_{k=1}^{K_m} \lambda_k^m(x) = 1\) 对每个 \(x \in X\) 都成立，故 \(f^m(x)\) 是点集 \((y_k^m)_{k=1}^{K_m}\) 的凸组合，又因为 \(X\) 是凸集，故 \(f^m(x)\) 的值域在 \(X\) 内。

第二步：运用布劳威尔不动点定理

对每个 \(m \in \mathbb{N}\)，\(f^m\) 都是连续的，因为它是有限个连续函数的和，根据布劳威尔不动点定理，\(f^m\) 至少有一个不动点 \(x^{*.m} \in X\) 满足 \(f^m(x^{*.m}) = x^{*.m}\)。因为不动点序列 \((x^{*.m})_{m \in \mathbb{N}}\) 包含在紧集 \(X\) 中，故存在一个收敛子列 \((x^{*.m_l})_{l \in \mathbb{N}}\)，收敛到一个点 \(x^* \in X\)。

第三步：\(x^*\) 是 \(F\) 的一个不动点

因为 \(x^{*.m_l}\) 是 \(f^{m_l}\) 的不动点，故

\[\begin{equation} x^{*.m_l} = f^{m_l}(x^{*.m_l}) = \sum\limits_{k=1}^{K_{m_l}} \lambda_k^{m_l}(x^{*.m_l}) y_k^{m_l} \tag{2} \label{kakutani} \end{equation}\]

此时我们需要利用前面的引理。对任意的 \(\varepsilon > 0\)，取符合引理条件的 \(\delta > 0\)，令 \(L\) 足够大使得对所有的 \(l \geqslant L\)，

\(\dfrac{1}{m_l} < \dfrac{\delta}{2}\)；
\(d(x^{*.m_l},x^*) < \dfrac{\delta}{2}\)。

令 \(l \geqslant L\)，对每个满足 \(\lambda_k^{m_l}(x^{*.m_l}) > 0\) 的 \(k\)，有 \(d(x_k^{m_l},x^{*.m_l}) < \dfrac{1}{m_l} < \dfrac{\delta}{2}\)（回忆 \(\lambda_k^m(x)\) 的定义），因此，根据三角不等式，对每个 \(k\) 有

\[d(x^*,x_k^{m_l}) \leqslant d(x^*,x^{*.m_l}) + d(x^{*.m_l},x_k^{m_l}) < \dfrac{\delta}{2} + \dfrac{\delta}{2} = \delta\]

根据引理，\(y_k^{m_l} \in F(x_k^{m_l}) \subseteq B(F(x^*),\varepsilon)\) 对任意的 \(k \in [K_m]\) 成立，即对任意的 \(k \in [K_m]\)，\(\lambda_k^{m_l}(x^{*.m_l}) = 0\) 或者 \(y_k^{m_l} \in B(F(x^*),\varepsilon)\)。因此，根据 \(\eqref{kakutani}\)，\(x^{*.m_l}\) 是凸集 \(B(F(x^*),\varepsilon)\) 的凸组合，即 \(x^{*.m_l} \in B(F(x^*),\varepsilon)\)。因为 \(\varepsilon\) 是任意的，且 \(F(x^*)\) 是闭集，故 \(x^* \in F(x^*)\)，即 \(x^*\) 是 \(F\) 的一个不动点。

不动点理论相关的历史

角谷不动点定理在 1941 年由角谷静夫提出，后来也有泛化为无穷维度局部凸拓扑向量空间的推广，称为角谷-格里科斯伯格-樊定理，对应的单值函数定理是吉洪诺夫不动点定理，具体的描述可以参考这个网页。还有一些其它的历史可以参考这个网页。

事实上不动点理论是一个曾经非常热门的方向，从布劳威尔不动点定理开始，1922 年，波兰著名数学家 S. Banach 给出了一个既简单又实用的压缩映射原理。此后也有越来越多的不动点定理研究成果涌现，除了这里讨论的角谷不动点定理外，还有例如 1968 年的 Fan-Browder 不动点定理，1972 年的 Himmelberg 不动点定理以及 Tarafdar 在 1987 年和 1992 年分别在拓扑线性空间和 H-空间建立的不动点定理；美国数学家 Michael（1956 年），Deutsch 和 Kenderov（1983 年），应用集值分析中的连续选择原理在拓扑空间建立集值不动点定理和几乎不动点定理；丹麦数学家 Nielsen 研究不动点的个数（Nielsen 数），开创不动点类理论的研究；1990 年以后，关于不动点理论的研究达到一个高潮，在各种映射或空间条件下，讨论不动点，随机不动点，几乎不动点等，每年有上百篇论文发表，新的不动点定理和各种迭代逼近方法不断涌现。

定理应用¶

我们将使用角谷不动点定理再次证明纳什定理，这事实上也是纳什本人使用的方法（见 Nash, J.F. (1950). Equilibrium Points in N-Person Games. Proceedings of the National Academy of Sciences of the United States of America）。我们同样令 \(\Gamma = (N,(\Sigma_i)_{i\in N},(U_i)_{i\in N})\)。

纳什定理

这一证明非常简单直接，因为我们只需要定义 \(F_i: \Sigma \to 2^{\Sigma_i}\) 为

\[F_i(\sigma) = \{\sigma_i \in \Sigma_i \mid U_i(\sigma_i,\sigma_{-i}) = \max\limits_{\sigma_i' \in \Sigma_i} U_i(\sigma_i',\sigma_{-i})\}\]

即 \(F_i(\sigma)\) 是参与人 \(i\) 对 \(\sigma_{-i}\) 的最优反应的集合。定义 \(F: \Sigma \to 2^{\Sigma}\) 满足 \(F(\sigma) = \mathop{\times}\limits_{i \in N} F_i(\sigma)\)。因为每个 \(F_i(\sigma)\) 是最优反应集合，根据混合策略的性质显然是闭凸集，故 \(F(\sigma)\) 是闭凸集，进一步显然 \(F\) 满足图像为闭集，因此符合角谷不动点定理的条件，存在 \(\sigma^* \in F(\sigma^*)\)，即 \(\forall i \in N\)，\(\sigma_i^* \in F_i(\sigma^*)\)，即 \(\sigma_i^*\) 是 \(\sigma_{-i}\) 的最优反应，故 \(\sigma^*\) 是一个混合策略纳什均衡。

因此我们只需要把集值函数直接定义为最优反应集合即可，那么不动点就是互为最优反应，因此这一证明相比于布劳威尔不动点定理的证明要简单许多，这也体现出角谷不动点定理的强大。

角谷静夫的小故事

在《纳什博弈论论文集》序言部分第七页最下边的注释，序言作者 Ken Binmore 讲了一个小故事，有次角谷静夫做演讲，演讲结束后，角谷静夫问 Kin Binmore 为啥这么多人来听演讲，Ken Binmore 解释说许多经济学家是来看作出如此重要的角谷静夫不动点理论的作者的。角谷静夫却回答说：“什么是角谷静夫不动点理论”。

KKM 定理¶

KKM 定理是拓扑学中的重要定理，是根据最早证明它的三位数学家的名字（Knaster-Kuratowski-Mazurkiewicz）命名的。KKM 定理实际上与布劳威尔不动点定理等价，这里我们先给出一个直接使用斯佩纳引理的证明，然后给出 KKM 定理和布劳威尔不动点定理的等价性证明。

KKM 定理

令 \(X_1,X_2,\cdots,X_n\) 是 \(X(n)\) 的紧子集，满足

并集是 \(X(n)\)，即 \(\bigcup\limits_{i=1}^n X_i = X(n)\)；
对于每个 \(i \in [n]\)，\(X_i \supseteq \{x = (x_1,\cdots,x_n) \in X(n) \mid x_i = 0\}\)。

那么它们的交集非空：\(\bigcap\limits_{i=1}^n X_i \neq \emptyset\)。

使用斯佩纳引理的证明需要引入一个概念，即相对开集：集合 \(A \subseteq \mathbb{R}^n\) 是集合 \(C \subseteq \mathbb{R}^n\) 的相对开集（relatively open set），如果存在一个开集 \(U \subseteq \mathbb{R}^n\)，使得 \(A = U \cap C\)。相应的我们也有相对闭集的概念，即 \(A\) 是 \(C\) 的相对闭集，如果 \(C \setminus A\) 是相对开集。

相对闭集的性质

根据闭集的性质，如果 \(A\) 是 \(C\) 的相对闭集，那么不难证明 \(A\) 的每个收敛于 \(C\) 内的序列的极限都在 \(A\) 中。原因很简单，根据定义相对闭集实际上也是一个闭集与 \(C\) 的交集，而闭集的极限点都在这一闭集内，所以如果极限点在 \(C\) 内，实际上就是在 \(C\) 与闭集的交集内，即在 \(A\) 内。

定理的证明

我们首先证明定理的特例，即 \((X_i)_{i=1}^n\) 是都是 \(X(n)\) 的相对开集的情况。使用反证法，设 \(\bigcap\limits_{i=1}^n X_i = \emptyset\)，因此对于任意的 \(x \in X(n)\)，都存在至少一个 \(i\) 使得 \(x \notin X_i\)。

对于每个 \(k \in \mathbb{N}\)，令 \(\mathcal{T}_k\) 是 \(X(n)\) 的划分，直径小于 \(\dfrac{1}{k}\)。定义 \(\mathcal{T_k}\) 的着色如下：对每个节点 \(y \in Y(\mathcal{T}_k)\)，\(y\) 的颜色是满足 \(y \notin X_i\) 的 \(i\) 之一。注意，如果 \(y_i = 0\)，那么 \(y \in X_i\)，故此时 \(y\) 的颜色不是 \(i\)。这意味着，如果 \(y\) 的颜色是 \(i\)，那么必然有 \(y_i > 0\)，即 \(y\) 的颜色是 \(y\) 的支撑中的一个指数，因此着色是合适的。根据斯佩纳引理，\(\mathcal{T}_k\) 中至少有一个完美着色的 \(n-1\) 维单纯形 \(T_k\)。这意味着对每个 \(i \in [n]\)，都存在 \(T_k\) 的一个顶点 \(x_{k,i}\)，其颜色为 \(i\)（故而不在 \(X_i\) 内）。

令 \(i \in [n]\)，考虑序列 \((x_{k,i})_{k \in \mathbb{N}}\)，因为 \(X(n)\) 是紧集，故存在子列收敛于 \(x_{*,i}\)。于是我们得到了 \(n\) 个极限值 \(x_{*,1},x_{*,2},\cdots,x_{*,n}\)，事实上，关于这些极限值，以下两个论断必然成立：

\(x_{*,i} = x_{*,j}\)，\(\forall i,j \in [n]\)；
\(x_{*,i} \notin X_i\)，\(\forall i \in [n]\)。

论断 1 表明，这些极限值必然都相等，即存在 \(x_{**} \in X(n)\) 满足 \(x_{*,i} = x_{**}\)，而论断 2 则说明 \(x_{**} \notin X_i,\forall i \in [n]\)，因此 \(x_{**} \notin \bigcup\limits_{i=1}^n X_i\)，这与 \(\bigcup\limits_{i=1}^n X_i = X(n)\) 矛盾！因此假设不成立，即 \(\bigcap\limits_{i=1}^n X_i \neq \emptyset\)。

事实上两个论断的证明并不复杂。对于论断 1，因为 \(x_{k,i}\) 在 \(T_k\) 内，而 \(\mathcal{T}_k\) 的直径小于 \(\dfrac{1}{k}\)，因此每个 \(x_{k,i}\) 和 \(x_{k,j}\) 之间的距离都小于 \(\dfrac{1}{k}\)，取 \(k \to \infty\) 即可得到结论。对于论断 2，因为 \(x_{k,i} \notin X_i\) 对于任意的 \(k \in \mathbb{N}\) 成立，并且 \(X_i\) 是相对开集，因此 \(X(n) \setminus X_i\) 是相对闭集，故根据相对闭集的性质，\(x_{*,i} \in X(n) \setminus X_i\)，即 \(x_{*,i} \notin X_i\)。

由此我们证明了 \((X_i)_{i=1}^n\) 是都是 \(X(n)\) 的相对开集的情况，这事实上覆盖了开集的情况，因此接下来证明 \((X_i)_{i=1}^n\) 是都是闭集的情况即可完成证明。对每个 \(\delta > 0\)，令 \(X_{i,\delta}\) 是 \(X_i\) 的 \(\delta\) 邻域，即 \(X_{i,\delta} = \{ x \in X(n) \mid d(x,X_i) < \delta \}\)。显然 \(X_{i,\delta}\) 在 \(X(n)\) 是相对开集，且包含 \(X_i\)。特别地，\(\bigcup\limits_{i=1}^n X_{i,\delta} \supseteq \bigcup\limits_{i=1}^n X_i = X(n)\)。根据特例的证明，\(\bigcap\limits_{i=1}^n X_{i,\delta}\) 非空，即存在 \(x_{\delta} \in X(n)\)，使得 \(x_{\delta} \in X_{i,\delta},\forall i \in [n]\)，特别地，\(d(x_\delta, X_i) < \delta\)。因为 \(X(n)\) 是紧集，因此存在 \((x_\delta)_{\delta > 0}\) 的子序列，收敛于一个极限（表示为 \(\hat{x}\)）。注意极限时，\(\delta \to 0\)，因此 \(d(\hat{x},X_i) = 0,\forall i \in [n]\)，即 \(\hat{x} \in X_i\)，因此 \(\hat{x} \in \bigcap\limits_{i=1}^n X_i\)，故 \(\bigcap\limits_{i=1}^n X_i \neq \emptyset\)。

总结而言，首先反证法，利用构造的染色产生了矛盾，从而证明了相对开集的情况，在闭集的情况则是取了闭集的邻域，把问题归约到了相对开集的情况，然后取极限完成证明。

接下来我们讨论 KKM 定理和布劳威尔不动点定理之间的等价性。首先我们从 KKM 定理出发证明布劳威尔不动点定理，这一侧比较简单，因为 KKM 的结果是交集非空，只要我们构造出交集是不动点的情况即可完成证明：

从 KKM 定理到布劳威尔不动点定理

\(f: X(n) \to X(n)\)，定义 \(X_i = \{x = (x_1,\cdots,x_n) \in X(n) \mid f_i(x) \geqslant x_i\}\)。

首先说明 \(\bigcup\limits_{i=1}^n X_i = X(n)\)：首先根据 \(X_i\) 的定义显然有 \(\bigcup\limits_{i=1}^n X_i \subseteq X(n)\)，因此只需证明 \(\bigcup\limits_{i=1}^n X_i \supseteq X(n)\)。事实上，对于任意的 \(x = (x_1,\cdots,x_n) \in X(n)\)，根据 \(f: X(n) \to X(n)\) 可知 \(\sum\limits_{i=1}^n x_i = \sum\limits_{i=1}^n f_i(x) = 1\)，因此不可能出现对于任意的 \(i \in [n]\) 都有 \(f_i(x) < x_i\) 的情况，故存在 \(i \in [n]\) 使得 \(f_i(x) \geqslant x_i\)，即存在 \(i \in [n]\) 使得 \(x \in X_i\)，得证。
对于每个 \(i \in [n]\)，\(X_i \supseteq \{x = (x_1,\cdots,x_n) \in X(n) \mid x_i = 0\}\) 是显然的。

因此根据 KKM，\(\bigcap\limits_{i=1}^n X_i = \{x = (x_1,\cdots,x_n) \in X(n) \mid f_i(x) \geqslant x_i, \forall i \in [n]\} \neq \emptyset\)，根据 \(\sum\limits_{i=1}^n x_i = \sum\limits_{i=1}^n f_i(x) = 1\) 可知，\(\bigcap\limits_{i=1}^n X_i = \{x = (x_1,\cdots,x_n) \in X(n) \mid f_i(x) = x_i, \forall i \in [n]\} \neq \emptyset\)，事实上这就表明了 \(f\) 至少有一个不动点。当然接下来将 \(f\) 的定义域推广到凸紧集与之前的方式一致，没有什么特别的。

接下来我们从布劳威尔不动点定理出发证明 KKM，相对而言会更加复杂，这里给出一个习题，相当于一个逐步得到最终证明的提示，提示后每一步都非常简单：

从布劳威尔不动点定理到 KKM 定理

仍然使用反证法，假设 \(\bigcap\limits_{i=1}^n X_i = \emptyset\)，

对每个 \(\varepsilon > 0\)，定义 \(Y^{i,\varepsilon} = \{x \in X(n) \mid d(x,X^i) \leqslant \varepsilon\}\)，证明：\(\bigcup\limits_{i=1}^n Y^{i,\varepsilon} = X(n)\) 对每个 \(\varepsilon > 0\) 成立，并且存在 \(\varepsilon_0 > 0\) 使得 \(\bigcap\limits_{i=1}^n Y^{i,\varepsilon_0} = \emptyset\)；
符号表示 \(Z^{i,\varepsilon} = X(n) \setminus Y^{i,\varepsilon}\)，证明：\(\sum\limits_{i=1}^n d(x,Z^{i,\varepsilon}) \geqslant \varepsilon\) 对每个 \(x \in X(n)\) 成立；
证明：\(\sum\limits_{i=1}^n x_id(x,Y^{i,\varepsilon}) = \sum\limits_{i: x \notin Y^{i,\varepsilon}} x_id(x,Y^{i,\varepsilon})\) 对每个 \(x \in X(n)\) 成立；
定义函数 \(f^\epsilon: X(n) \to X(n)\) 为 \(f^\epsilon_i(x) = {\begin{cases} x_i - x_id(x,Y^{i,\varepsilon}) & \text{如果 } x \notin Y^{i,\varepsilon} \\ x_i + (\sum\limits_{i=1}^n x_id(x,Y^{i,\varepsilon}))\dfrac{d(x,Z^{i,\varepsilon})}{\sum\limits_{i=1}^n d(x,Z^{i,\varepsilon})} & \text{如果 } x \in Y^{i,\varepsilon} \end{cases}}\)，证明：\(f^\epsilon\) 是连续函数，值域在 \(X(n)\) 内，且 \(f^\epsilon\) 有一个不动点 \(x^\varepsilon\)；
证明：\(x^\varepsilon \in \bigcap\limits_{i=1}^n Y^{i,\varepsilon}\)；
令 \((\epsilon_k)_{k \in \mathbb{N}}\) 是收敛于 \(0\) 的序列，使得 \(x^* = \lim\limits_{k \to \infty} x^{\epsilon_k}\) 存在，证明：\(x^* \in \bigcap\limits_{i=1}^n X_i\)，与假设矛盾。