社会选择理论¶

在之前的研究中，我们通常考虑的是个体的偏好、效用理论，而在本讲，我们将分析在多大程度上个人偏好能被加总为社会偏好，或者更直接地，被加总为社会决策，并且这种加总方式要“令人满意”，即需要满足一系列合意条件。我们从最简单的备选方案只有两种的情况开始，此时我们可以找到很多令人满意的加总方式，但是当备选方案的数量增多时，我们的讨论急转直下，这也就引入了著名的阿罗不可能定理，随后我们会介绍两种走出不可能定理困境的方法。最后我们会介绍如何直接将个人偏好加总为社会决策，引入社会选择函数的概念。

特殊情形：两种备选方案上的社会偏好¶

自然地，我们从最简单的备选方案只有两种的情况开始。我们将这些备选方案称为 \(x\) 和 \(y\)，例如方案 \(x\) 可能是“维持现状”，而 \(y\) 是正在讨论准备实施的某个公共项目。

对于我们的问题，我们拥有的资料是社会成员在这两个备选方案上的个人偏好。我们假设个人或称参与人（agents）的数量为 \(I < \infty\) 个。个人在这两个方案上的偏好集可用组合 \((\alpha_1, \cdots, \alpha_I) \in \mathbb{R}^I\) 来表示，其中 \(\alpha_i \in \{-1, 0, 1\}\)，分别表示个人 \(i\) 偏好 \(x\) 胜于 \(y\)、无差异以及偏好 \(y\) 胜于 \(x\)。

需要注意的是，在本讲中我们始终假设，在备选方案的社会决策问题中，真正重要的仅为参与人对备选方案的偏好排序，而不是他们的偏好程度（即不涉及基数或强度信息），因此我们排除了不同人之间快乐或痛苦感的比较。

定义 1：社会福利泛函数

一个社会福利泛函数（social welfare functional）或称社会福利加总器（social welfare aggregator）是一个规则 \(F(\alpha_1, \cdots, \alpha_I)\)，该规则对个人偏好的每个可能组合 \((\alpha_1, \cdots, \alpha_I) \in \{-1,0,1\}^I\) 都指定了一个社会偏好，即 \(F(\alpha_1, \cdots, \alpha_I) \in \{-1, 0, 1\}\)。

接下来我们将考察社会福利泛函数应当满足的性质，首先我们考察的所有社会福利函数都要在下面定义 2 的弱意义上尊重个人偏好：

定义 2：帕累托性质

社会福利泛函数 \(F(\alpha_1, \cdots, \alpha_I)\) 是帕累托的（Paretian）或称为具有帕累托性质（Pareto property），如果它尊重参与人严格偏好的一致性，也就是说，如果 \(F(1, \cdots, 1) = 1\) 和 \(F(-1, \cdots, -1) = -1\)。

因此满足帕累托性质，也就是当所有人都严格偏好 \(x\) 时，社会也严格偏好 \(x\)，当所有人都严格偏好 \(y\) 时，社会也严格偏好 \(y\)。这显然是一个自然的要求，否则社会的决策将会违背所有人的意愿。

例 1：多数投票

两个备选方案之间的帕累托社会福利泛函数比比皆是。令 \((\beta_1, \cdots, \beta_I) \in \mathbb{R}^I\) 是个元素非负的向量而且不是零向量。于是我们可以定义

\[ F(\alpha_1, \cdots, \alpha_I) = \text{sign} \sum_{i=1}^I \beta_i \alpha_i. \]

其中 \(\text{sign}\) 是符号函数，即对于任何 \(a \in \mathbb{R}\)，根据 \(a > 0, a = 0\) 或 \(a < 0\)，\(\text{sign } a\) 分别等于 \(1, 0\) 或 \(-1\)。

一个重要的特殊情形是多数投票（majority voting），也就是说，投票表决且多数票获胜。相信读者应该都不难看出当我们取 \(\beta_i = 1,\ \forall i\) 时就是多数投票规则。于是 \(F(\alpha_1, \cdots, \alpha_I) = 1\) 当且仅当偏好 \(x\) 胜于 \(y\) 的人数多于偏好 \(y\) 胜于 \(x\) 的人数。类似地，\(F(\alpha_1, \cdots, \alpha_I) = -1\) 当且仅当偏好 \(y\) 胜于 \(x\) 的人数多于偏好 \(x\) 胜于 \(y\) 的人数。最后，\(F(\alpha_1, \cdots, \alpha_I) = 0\) 当且仅当偏好 \(x\) 胜于 \(y\) 的人数等于偏好 \(y\) 胜于 \(x\) 的人数，此时两种选择社会无差异。

定义 3：独裁

我们说一个社会福利泛函数是独裁的（dictatorial），如果存在一个参与人（独裁者），使得对于任何组合 \((\alpha_1, \cdots, \alpha_I)\)，\(\alpha_i = 1\) 意味着 \(F(\alpha_1, \cdots, \alpha_i) = 1\)，而且类似地，\(\alpha_i = -1\) 意味着 \(F(\alpha_1, \cdots, \alpha_i) = -1\)。也就是说，独裁者的偏好成为了社会偏好。独裁的社会福利泛函数在定义 2 的意义上具有帕累托性质。对于例 1 中的社会福利泛函数，只要对于某个参与人 \(i\) 有 \(\beta_i > 0\) 以及当 \(j \neq i\) 时 \(\beta_j = 0\)，我们就得到了一个独裁关系，因为 \(F(\alpha_1, \cdots, \alpha_I) = \text{sign }\beta_i\alpha_i,\ \beta_i > 0\)。

多数投票社会福利泛函数在社会选择理论中扮演着重要的基准角色。除了具有帕累托性质之外，它还具有其他三个重要性质，下面我们将正式阐述这些性质。第一个性质（参与人之间的对称性）是说社会福利泛函数平等对待每个参与人。类似地，第二个性质（备选方案的中立性）是说，社会福利泛函数事先不偏重任何一个备选方案。第三个性质（正反应性）比定义 2 的帕累托性质更强，它是说社会福利泛函数对个人偏好比较敏感。

定义 4：对称性

社会福利泛函数 \(F(\alpha_1, \cdots, \alpha_I)\) 在参与人之间是对称的（symmetric）或称为匿名的（anonymous），如果参与人的名字并不重要，即，如果将各参与人的偏好重新排列不会改变社会偏好。准确地说，令 \(\pi: \{1, \cdots, I\} \rightarrow \{1, \cdots, I\}\) 是个满射函数（即，该函数具有下列性质：对于任何 \(i\) 存在 \(h\) 使得 \(\pi(h) = i\)）。那么对于任何组合 \((\alpha_1, \cdots, \alpha_r)\) 我们有 \(F(\alpha_1, \cdots, \alpha_r) = F(\alpha_{\pi(1)}, \cdots, \alpha_{\pi(I)})\)。

对称性（或匿名性）使得我们自然地会想起 Shapley 值的对称性，这是一个很自然的要求，因为在很多决策情况下（如无记名投票）参与人的名字本身并不应该影响社会的决策。

定义 5：中立性

社会福利泛函数 \(F(\alpha_1, \cdots, \alpha_I)\) 在备选方案之间是中立性的（neutral），如果对于每个组合 \((\alpha_1, \cdots, \alpha_I)\) 都有 \(F(\alpha_1, \cdots, \alpha_I) = -F(-\alpha_1, \cdots, -\alpha_I)\) 成立。也就是说，如果我们颠倒所有参与人的偏好，社会偏好也会颠倒。

中立性也不难理解，因为如果这一条件不成立，那么就会出现即使所有人偏好颠倒，社会偏好却不变的情况（并且社会偏好不是无差异的），那么显然此时社会是偏好这一不变的决策的。

定义 6：正反应性

社会福利泛函数 \(F(\alpha_1, \cdots, \alpha_I)\) 是正反应的（positively responsive），如果当 \((\alpha_1, \cdots, \alpha_I) \geqslant (\alpha_1', \cdots, \alpha_I')\)，\((\alpha_1, \cdots, \alpha_I) \neq (\alpha_1', \cdots, \alpha_I')\) 以及 \(F(\alpha_1', \cdots, \alpha_I') \geqslant 0\) 时，我们有 \(F(\alpha_1, \cdots, \alpha_I) = 1\)。也就是说，如果社会认为 \(x\) 优于 \(y\) 或与 \(y\) 一样好而且某些参与人开始看重 \(x\)，那么 \(x\) 是受社会偏好的。

容易验证多数投票满足参与人间对称性、备选方案间中立性以及正反应性这三个性质。更强的结论是，反之我们也可以证明，这些性质完全刻画了多数投票：

May 定理（1952）

一个社会福利泛函数 \(F(\alpha_1, \cdots, \alpha_I)\) 是个多数投票社会福利函数当且仅当它在参与人之间是对称的、在备选方案间是中立性的以及是正反应的。

May 定理的证明

为了证明：我们已经说过多数投票满足这三个性质，这就是必要性。为了证明充分性，注意到参与人之间的对称性意味着社会偏好仅取决于偏好 \(x\) 胜于 \(y\) 的参与人总数、认为 \(x\) 与 \(y\) 无差异的参与人总数以及偏好 \(y\) 胜于 \(x\) 的参与人总数。给定 \((a_1, \cdots, a_r)\)，记

\[ n_+(a_1, \cdots, a_r) = \# \{i: \alpha_i = 1\} \quad \text{和} \quad n_-(a_1, \cdots, \alpha) = \# \{i: \alpha_i = -1\} \]

参与人之间的对称性能让我们将 \(F(a_1, \cdots, \alpha_1)\) 写为

\[ F(\alpha_1, \cdots, \alpha_I) = G(n_+(\alpha_1, \cdots, \alpha_I), n_-(\alpha_1, \cdots, \alpha_I)) \]

现在假设 \((\alpha_1, \cdots, \alpha_I)\) 使得 \(n_+(\alpha_1, \cdots, \alpha_I) = n_-(\alpha_1, \cdots, \alpha_I)\)。于是 \(n_+(-\alpha_1, \cdots, -\alpha_I) = n_-(\alpha_1, \cdots, \alpha_I) = n_+(\alpha_1, \cdots, \alpha_I) = n_-(-\alpha_1, \cdots, -\alpha_I)\)，因此

\[ \begin{aligned} F(\alpha_1, \cdots, \alpha_I) &= G(n_+(\alpha_1, \cdots, \alpha_I), n_-(\alpha_1, \cdots, \alpha_I)) \\ &= G(n_+(-\alpha_1, \cdots, -\alpha_I), n_-(-\alpha_1, \cdots, -\alpha_I)) \\ &= F(-\alpha_1, \cdots, -\alpha_I) \\ &= -F(\alpha_1, \cdots, \alpha_I) \end{aligned} \]

最后一个等式可由备选方案之间的中立性推出。我们已经知道，对于一个数来说，如果它等于它的相反数，那么这个数必定为零。因此，我们断言，如果 \(n_+(\alpha_1, \cdots, \alpha_I) = n_-(\alpha_1, \cdots, \alpha_I)\)，那么 \(F(\alpha_1, \cdots, \alpha_I) = 0\)。

接下来假设 \(n_+(\alpha_1, \cdots, \alpha_I) > n_-(\alpha_1, \cdots, \alpha_I)\)。记 \(H = n_+(\alpha_1, \cdots, \alpha_I)\)，\(J = n_-(\alpha_1, \cdots, \alpha_I)\)；于是 \(J < H\)。不失一般性，令 \(\alpha_i = 1\) 对于 \(i \leqslant H\)；\(\alpha_i \leqslant 0\) 对于 \(i > H\)。考虑一个新组合 \((\alpha_1', \cdots, \alpha_I')\)，该组合由 \(\alpha_i' = \alpha_i = 1\) 对于 \(i \leqslant J < H\)，\(\alpha_i' = 0\) 对于 \(J < i \leqslant H\)，以及 \(\alpha_i' = \alpha_i \leqslant 0\) 对于 \(i > H\) 所定义。于是，\(n_+(\alpha_1', \cdots, \alpha_I') = J\) 和 \(n_-(\alpha_1', \cdots, \alpha_I') = n_-(\alpha_1, \cdots, \alpha_I) = J\)。因此，根据前面得到的结论 \(F(\alpha_1', \cdots, \alpha_I') = 0\)。但是根据我们的构造，备选方案 \(x\) 在新个人偏好中已经失宠了。的确，\((\alpha_1, \cdots, \alpha_I) \geqslant (\alpha_1', \cdots, \alpha_I')\) 和 \(\alpha_{J+1} = 1 > 0 = \alpha_{J+1}'\)。因此，根据正反应性可知，我们必定有 \(F(\alpha_1, \cdots, \alpha_I) = 1\)。

反过来，如果 \(n_-(\alpha_1, \cdots, \alpha_I) > n_+(\alpha_1, \cdots, \alpha_I)\)，那么 \(n_+(-\alpha_1, \cdots, -\alpha_I) > n_-(\alpha_1, \cdots, \alpha_I)\)，于是 \(F(-\alpha_1, \cdots, -\alpha_I) = 1\)，从而 \(F(\alpha_1, \cdots, \alpha_I) = -1\)。由此我们可以断言 \(F(\alpha_1, \cdots, \alpha_I)\) 的确是个多数投票社会福利泛函数。

上述证明的关键总结如下：

根据对称性直接得到 \(F\) 只能与 \(n_+\) 和 \(n_-\) 有关；
构造 \(n^+ = n^-\) 的情况，根据中立性得到 \(F = 0\)；
构造 \(n^+ > n^-\) 的情况，根据正反应性以及第 2 点的结果得到 \(F = 1\)（因此说正反应性比帕累托性质更强）。

一般情形：阿罗不可能定理¶

下面我们研究任何数量备选方案上个人偏好的加总问题。我们将备选方案集合记为 \(X\)，并且假设有 \(I\) 个参与人 \(i = 1,\cdots, I\)。每个参与人 \(i\) 有着定义在 \(X\) 上的理性（即满足完备性和传递性）偏好关系 \(\succeq_i\)。我们将从 \(\succeq_i\) 推导出的严格偏好和无差异关系分别记为 \(\succ_i\) 和 \(\sim_i\)。另外，为方便起见，我们经常假设在个人偏好关系中任何两个不同的方案都不是无差异的。因此，为了区别这两种情形，我们将 \(X\) 上的所有可能理性偏好关系组成的集合记为 \(\mathcal{R}\)，而将满足不存在两个不同备选方案是无差异性质的 \(X\) 上的所有可能理性偏好关系组成的集合记为 \(\mathcal{P}\)。注意到 \(\mathcal{P} \subset \mathcal{R}\)。

正式地说，偏好关系 \(\succeq_i \in \mathcal{P}\)，如果它是自反（即 \(x \succeq_i x\) 对于所有 \(x \in X\)）、传递以及全域（total）的（若 \(x \neq y\)，则要么 \(x \succeq_i y\)，要么 \(y \succeq_i x\)，但不可能都成立）。这样的偏好关系通常称为严格-全面（strict- total）偏好，或称*线性序（linear orders），因为这些性质就是实直线通常拥有的序：“大于或等于”关系。

类似于上一小节，我们可以将社会福利泛函数定义为一个规则，该规则对个人偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{R}^I\) 指定了一个社会偏好。下面的定义 7 在两个方面推广了定义 1：一是它允许任何数量的备选方案；二是它允许将加总问题限制在个人偏好组合的某个给定定义域 \(\mathcal{A} \subset \mathcal{R}^I\)。然而在本节我们主要考察最大的定义域，即 \(\mathcal{A} = \mathcal{R}^I\) 和 \(\mathcal{A} = \mathcal{P}^I\)。

定义 7：社会福利泛函数

定义在给定子集 \(\mathcal{A} \subset \mathcal{R}^I\) 的一个社会福利泛函数（或称社会福利加总器）是一个规则 \(F: \mathcal{A} \to \mathcal{R}\)，该规则对可行定义域 \(\mathcal{A} \subset \mathcal{R}^I\) 中的个人理性偏好关系的任何组合 \((\succeq_1, \cdots, \succeq_I)\) 指定了一个理性偏好关系 \(F(\succeq_1, \cdots, \succeq_I) \in \mathcal{R}\)，这个理性偏好关系称为社会偏好关系。

注意到，正如我们在上一节的做法一样，在社会加总问题中，个人特征完全是由他们在备选方案上的偏好关系刻画的，不考虑偏好的强度等。进一步地，对于任何组合 \((\succeq_1, \cdots, \succeq_I)\)，我们将由 \(F(\succeq_1, \cdots, \succeq_I)\) 导出的严格偏好关系记为 \(F_p(\succeq_1, \cdots, \succeq_I)\)，读作社会认为 \(x\) 比 \(y\) 好。

下面的定义 8 是定义 2 的推广，它要求社会福利泛函数在下面的弱意义上尊重个人偏好：

定义 8：帕累托性质

一个社会福利泛函数 \(F: \mathcal{A} \to \mathcal{R}\) 是帕累托的（Paretian），如果对于任何一对备选方案 \(\{x,y\} \in X\) 和任何偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\)，如果 \(x \succ_i y\) 对于每个 \(i\) 成立，那么 \(x F_p(\succeq_1, \cdots, \succeq_I) y\)。

下面的例子描述了一类著名且有趣的帕累托社会福利泛函数：

例 2：波达计分

波达计分（Borda Count）：假设备选方案数量是有限的。给定一个偏好关系 \(\succeq_i \in \mathcal{R}\)，我们按照以下规则对每个备选方案 \(x \in X\) 指定一个分数。暂时假设在偏好关系 \(\succeq_i\) 中任何两个备选方案都不是无差异的。于是我们令 \(c_i(x) = n\)，如果 \(x\) 在 \(\succeq_i\) 的序中位于第 \(n\) 名。如果在 \(\succeq_i\) 中允许无差异，那么 \(c_i(x)\) 是与 \(x\) 无差异的备选方案的平均排名。例如，如果 \(X = \{x,y,z\}\)，而且 \(x \succ_i y \sim_i z\)，那么 \(c_i(x) = 1\)，\(c_i(y) = c_i(z) = 2.5\)。

最后，对于任何组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{R}\)，我们通过将分数加总得到它的社会排序。也就是说，如果 \(\sum\limits_{i} c_i(x) \leqslant \sum\limits_{i} c_i(y)\)，那么 \(x \succeq y\)。我们令 \(F(\succeq_1, \cdots, \succeq_I) \in \mathcal{R}\) 表示由 \(x F(\succeq_1, \cdots, \succeq_I) y\) 定义的偏好关系，那么显然这个偏好关系是完备的和传递的（它可由效用函数 \(c(x) = -\sum\limits_{i} c_i(x)\) 表示）。而且，该偏好关系是帕累托的，这是因为如果 \(x \succ_i y\) 对于每个 \(i\)，那么 \(c_i(x) < c_i(y)\) 对于每个 \(i\)，从而有 \(\sum\limits_{i} c_i(x) < \sum\limits_{i} c_i(y)\)。

下面我们阐述社会福利泛函数面对的一个重要限制条件，它首先由 Arrow（1963）提出。这个限制条件指出任何两个备选方案上的社会偏好仅取决于这两个方案上的个人偏好。我们可从三个方面为这个假设辩护：

首先，它认为在确定 \(x\) 与 \(y\) 的社会排序时，是否存在其他方案是不重要的，这些其他方案与当前的问题无关。这个理由是严格规范的而且有相当的吸引力；
第二个理由是实践性的。这个假设使得社会决策任务变得非常方便，因为它有助于隔离问题。在确定某个备选方案子集的社会排序时，我们不需要这个子集之外的任何个人偏好信息；
第三个理由与激励有关，我们将在本讲最后一小节的无谎报的激励命题中讨论。下面定义的配对独立性（pairwise independence）性质与如何提供激励让个人如实显示自己的偏好这个问题密切相关。

定义 9：配对独立性

定义域为 \(\mathcal{A}\) 的社会福利泛函数 \(F: \mathcal{A} \to \mathcal{R}\) 满足配对独立性条件（pairwise independence condition）或称不相关方案无关性条件（independence of irrelevant alternative condition），如果任何两个备选方案 \(\{x,y\} \in X\) 上的社会偏好仅取决于这两个方案上的个人偏好组合。正式地说，对于任何一对备选方案 \(\{x,y\} \in X\)，以及对于具有下列性质的任何一对偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\) 和 \((\succeq_1', \cdots, \succeq_I') \in \mathcal{A}\)，即对于每个 \(i\)，如果

\[x \succeq_i y \iff x \succeq_i' y \quad \text{和} \quad y \succeq_i x \iff y \succeq_i' x,\]

我们都有

\[x F_p(\succeq_1, \cdots, \succeq_I) y \iff x F_p(\succeq_1', \cdots, \succeq_I') y \quad \text{和} \quad y F_p(\succeq_1, \cdots, \succeq_I) x \iff y F_p(\succeq_1', \cdots, \succeq_I') x.\]

这一定义的表达看起来有些啰嗦，我们这么做的原因无非就是强调它前面的陈述。用通俗的语言解释就是，两个不同的偏好组合只要在 \(x\) 与 \(y\) 上的偏好关系一致，那么社会对 \(x\) 与 \(y\) 的偏好也应该一致。等价的表达为：对于任何 \(\{x,y\} \subset X\)，若 \(\succeq_i \vert \{x,y\} = \succeq_i' \vert \{x,y\}\) 对于所有 \(i\) 成立，那么 \(F(\succeq_1, \cdots, \succeq_I) \vert \{x,y\} = F(\succeq_1', \cdots, \succeq_I') \vert \{x,y\}\)。此处 \(\succeq \vert \{x,y\}\) 表示将偏好排序 \(\succeq\) 限制在集合 \(\{x,y\}\) 上。

例 2：波达计分（续）

波达计分不满足配对独立性条件。原因很简单：任何一个备选方案的位次都取决于每个其他备选方案的位次。或者说，排序是有数字大小的，这会影响到配对独立性。例如，假设有两个参与人和三个备选方案 \(\{x,y,z\}\)。对于偏好

\[\begin{gather*} x \succ_1 y \succ_1 z, \\ y \succ_2 x \succ_2 z, \end{gather*}\]

那么社会认为 \(x\) 比 \(y\) 好，因为 \(c(x) = 3, c(y) = 4\)，但是对于偏好

\[\begin{gather*} x \succ_1' y \succ_1' z, \\ y \succ_2' z \succ_2' x, \end{gather*}\]

社会认为 \(y\) 比 \(x\) 好，因为 \(c(x) = 4, c(y) = 3\)。然而对每个参与人而言，\(x\) 和 \(y\) 的相对位次没有改变。

上面例子的讨论表明，配对独立性条件是个重要限制。然而，有一种自然的方法能保证这个条件自动满足：我们可以通过某种特定加总规则来确定任何给定的两个备选方案之间的社会偏好，这个加总规则只使用了个人偏好中这两个方案的排序信息，从而我们可以得到任意一对备选方案之间的偏好关系，且是独立于其它备选方案的。并且在上一节我们已经看到，对于任何一对备选方案，存在很多这样的规则（例如多数投票）。我们能否按照这种配对方式实施而且仍能得到理性（即完备且传递的）社会偏好？下面的例子表明这非常困难：

例 3：康多塞悖论

康多塞悖论（Condorcet Paradox）：假设我们要在两个备选方案之间进行多数投票。我们能否确定一个社会福利泛函数？在下一节我们将看到在某个受限制定义域 \(\mathcal{A} \subset \mathcal{R}^I\) 内答案是肯定的。但在一般情形下我们将遇到所谓的康多塞悖论难题。假设我们有三个备选方案 \(\{x,y,z\}\) 和三个参与人。这三个人的偏好为

\[\begin{gather*} x \succ_1 y \succ_1 z, \\ y \succ_2 z \succ_2 x, \\ z \succ_3 x \succ_3 y. \end{gather*}\]

多数投票规则告诉我们社会认为 \(x\) 比 \(y\) 好（因为认为 \(x\) 胜过 \(y\) 的人数多于 \(y\) 胜过 \(x\) 的人数），\(y\) 比 \(z\) 好，以及 \(z\) 比 \(x\) 好，但这样的循环模式违背了社会偏好的传递性条件。

下一个命题是阿罗不可能定理，该定理是本章的核心结果。它在本质上告诉我们，康多塞悖论的出现不是由多数投票的任何强性质（参与人之间的对称性、备选方案的中立性和正反应性）引起的。康多塞悖论点破了关键问题所在：在配对独立性条件下，不存在定义在 \(\mathcal{R}^I\) 上的社会福利泛函数，使得该函数满足最低形式的参与人之间的对称性（无独裁者）和最低形式的正反应性（帕累托性质）。

阿罗不可能定理（Arrow's Impossibility Theorem）

假设至少有三个备选方案，个人组合的定义域 \(\mathcal{A}\) 要么为 \(\mathcal{A} = \mathcal{R}^I\)，要么为 \(\mathcal{A} = \mathcal{P}^I\)。那么每个满足帕累托性质和配对独立性条件的社会福利泛函数 \(F: \mathcal{A} \to \mathcal{R}\) 在下列意义上是独裁的：存在一个参与人 \(h\) 使得对于任何 \(\{x,y\} \subset X\) 和任何组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\)，当 \(x \succ_h y\) 时，社会认为 \(x\) 比 \(y\) 好，即 \(x F_p(\succeq_1, \cdots, \succeq_I) y\)。

为证明的方便起见，我们将 \(I\) 不仅视为参与人的数量，也视为参与人集合。对于整个证明，我们使用一个满足帕累托性质和配对独立性条件的固定社会福利泛函数 \(F: \mathcal{A} \to \mathcal{R}\)。我们先给出一些定义，这些定义是证明的关键：

定义 10：决定性

给定 \(F(·)\)，对于参与人集合的一个子集 \(S \subset I\)，

如果当 \(S\) 中的每个人认为 \(x\) 比 \(y\) 好且 \(S\) 之外的每个人认为 \(y\) 比 \(x\) 好，导致社会认为 \(x\) 比 \(y\) 好，那么我们说 \(S\) 可以决定 \(x\) 比 \(y\) 好（decisive for \(x\) over \(y\)）；
如果对于任何一对备选方案 \(\{x,y\} \subset X\)，\(S\) 可以决定 \(x\) 比 \(y\) 好，那么我们说 \(S\) 是决定性的（decisive）；
如果当 \(S\) 中的每个人认为 \(x\) 比 \(y\) 好，导致社会认为 \(x\) 比 \(y\) 好，那么我们说 \(S\) 完全可以决定 \(x\) 比 \(y\) 好（completely decisive for \(x\) over \(y\)）。

我们的证明将沿着详细考察决定集族的结构这个路线进行。我们分步骤完成这个任务。第 1 步到第 3 步表明，如果某个参与人子集对于某对方案是决定性的，那么它对所有配对方案都是决定性的。第 4 步到第 6 步证明了决定集族的一些代数性质。第 7 步和第 8 步使用这些性质证明了存在由单个参与人组成的最小决定集。第 9 步和第 10 步证明这个参与人是个独裁者。

阿罗不可能定理的证明

第 1 步：如果对于某个 \(\{x,y\} \subset X\)，\(S \subset I\) 可以决定 \(x\) 比 \(y\) 好，那么对于任何备选方案 \(z \neq x\)，\(S\) 可以决定 \(x\) 比 \(z\) 好。类似地，对于任何 \(z \neq y\)，\(S\) 可以决定 \(z\) 比 \(y\) 好。

我们仅如果 \(S\) 可以决定 \(x\) 比 \(y\) 好，那么 \(S\) 可以决定 \(x\) 比 \(z \neq x\) 好。另一部分的证明是类似的。如果 \(z = y\)，我们就不用证明了。因此，我们假设 \(z \neq y\)。考虑一个偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\)，其中

\[\begin{gather*} x \succ_i y \succ_i z, \ \forall i \in S, \\ y \succ_i z \succ_i x, \ \forall i \in I \setminus S. \end{gather*}\]

由于 \(S\) 可以决定 \(x\) 比 \(y\) 好，所以社会认为 \(x\) 比 \(y\) 好，也就是说 \(x F_p(\succeq_1, \cdots, \succeq_I) y\)。另一方面，由于 \(y \succ_i z\) 对于每个 \(i \in I\) 成立，所以根据 \(F\) 满足帕累托性质可知 \(y F_p(\succeq_1, \cdots, \succeq_I) z\)。因此，由社会偏好的传递性可知 \(x F_p(\succeq_1, \cdots, \succeq_I) z\)。

根据配对独立性条件，只要 \(S\) 中的每个人认为 \(x\) 比 \(z\) 好且 \(S\) 之外的每个人认为 \(z\) 比 \(x\) 好，那么社会就会和上面我们举的这一特殊偏好例子一样认为 \(x\) 比 \(z\) 好。因此，\(S\) 可以决定 \(x\) 比 \(z\) 好。

注：这里的证明思想是找到一种特殊的偏好关系证明在这种偏好下 \(S\) 可以决定 \(x\) 比 \(z\) 好，然后根据配对独立性推广到其它的偏好关系都能做到这一点，因为其它的偏好关系只要保持 \(x\) 和 \(z\) 在 \(S\) 和 \(I \setminus S\) 下的顺序和前面的特殊偏好关系一致，根据配对独立性就能说明社会认为 \(x\) 比 \(z\) 好，因此根据定义可知 \(S\) 可以决定 \(x\) 比 \(z\) 好，这一思想在之后的证明中很常用。

第 2 步：如果对于某个 \(\{x,y\} \subset X\)，\(S \subset I\) 可以决定 \(x\) 比 \(y\) 好，\(z\) 是第三个备选方案，那么当 \(w \in X\) 是不同于 \(z\) 的任何备选方案时，\(S\) 可以决定 \(z\) 比 \(w\) 好以及决定 \(w\) 比 \(z\) 好。

根据第 1 步，\(S\) 可以决定 \(x\) 比 \(z\) 好以及决定 \(z\) 比 \(y\) 好。如果我们再次使用第 1 步，只不过这次运用在 \(\{x,z\}\) 和 \(w\) 上，可知：\(S\) 可以决定 \(w\) 比 \(z\) 好。类似地，将第 1 步运用在 \(\{z,y\}\) 和 \(w\) 上，可知：\(S\) 可以决定 \(z\) 比 \(w\) 好。

第 3 步：如果对于某个 \(\{x,y\} \subset X\)，\(S \subset I\) 可以决定 \(x\) 比 \(y\) 好，那么 \(S\) 是决定性的。

取任意的 \(\{v,w\} \subset X\)。如果 \(v = z\) 或 \(v = w\)，那么第 2 步直接蕴含了第 3 步的结论。如果 \(v \neq z\) 且 \(w \neq z\)，我们可以运用第 2 步从而断言 \(S\) 可以决定 \(z\) 比 \(w\) 好，然后使用第 1 步（运用在 \(\{z,w\}\) 上）断言 \(S\) 可以决定 \(v\) 比 \(w\) 好。

第 4 步：如果 \(S\) 和 \(T\) 是决定性的，那么 \(S \cap T\) 是决定性的。

任取三个不同的备选方案 \(\{x,y,z\} \subset X\)，考虑偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\)，其中

\[\begin{align*} z \succ_i y \succ_i x, \ &\forall i \in S \setminus (S \cap T), \\ x \succ_i z \succ_i y, \ &\forall i \in S \cap T, \\ y \succ_i x \succ_i z, \ &\forall i \in T \setminus (S \cap T), \\ y \succ_i z \succ_i x, \ &\forall i \in I \setminus (S \cup T). \end{align*}\]

于是 \(z F_p(\succeq_1, \cdots, \succeq_I) y\)，因为 \(S = [S \setminus (S \cap T)] \cup (S \cap T)\) 是决定性的。类似地，\(x F_p(\succeq_1, \cdots, \succeq_I) z\)，因为 \(T\) 是决定性的。因此，根据社会偏好的传递性可知 \(x F_p(\succeq_1, \cdots, \succeq_I) y\)。而在上述偏好关系下，当 \(i \in S \cap T\) 时，\(x \succ_i y\)，当 \(i \in I \setminus (S \cup T)\) 时，\(y \succ_i x\)，因此在这一偏好关系下 \(S \cap T\) 可以决定 \(x\) 比 \(y\) 好。由配对独立性条件可知，在更大的偏好关系集合下 \(S \cap T\) 可以决定 \(x\) 比 \(y\) 好。最后由第 3 步的结论可知 \(S \cap T\) 是决定性的。

第 5 步：对于任何 \(S \subset I\)，我们有：要么 \(S\) 是决定性的，要么 \(I \setminus S\) 是决定性的。

任取三个不同的备选方案 \(\{x,y,z\} \subset X\)，考虑偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\)，其中

\[\begin{align*} x \succ_i z \succ_i y, \ &\forall i \in S, \\ y \succ_i x \succ_i z, \ &\forall i \in I \setminus S. \end{align*}\]

于是存在两种可能性：一是 \(x F_p(\succeq_1, \cdots, \succeq_I) y\)，在这种情形下，根据配对独立性条件可知，\(S\) 可以决定 \(x\) 比 \(y\) 好（由第 3 步的结论可知 \(S\) 是决定性的）；二是 \(y F_p(\succeq_1, \cdots, \succeq_I) x\)，因为根据帕累托性质条件，我们有 \(x F_p(\succeq_1, \cdots, \succeq_I) z\)，在这种情形下，社会偏好关系产生了 \(y F_p(\succeq_1, \cdots, \succeq_I) z\)。再次使用配对独立性条件，我们断言 \(I \setminus S\) 可以决定 \(y\) 比 \(z\) 好（由第 3 步可知 \(I \setminus S\) 是决定性的）。

第 6 步：如果 \(S \subset I\) 是决定性的而且 \(S \subset T\)，那么 \(T\) 也是决定性的。

根据帕累托性质条件可知，如果参与人集合是空集，那么它不可能是决定性的（的确，如果没有人认为 \(x\) 比 \(y\) 好并且每个人认为 \(y\) 比 \(x\) 好，那么社会不会认为 \(x\) 比 \(y\) 好）。因此，\(I \setminus T\) 不可能是决定性的，因为如若不然，根据第 4 步可知，\(S \cap (I \setminus T) = \emptyset\) 将是决定性的。因此，由第 5 步可知，\(T\) 是决定性的。

第 7 步：如果 \(S \subset I\) 是决定性的而且它含有不止一个参与人，那么存在一个严格子集 \(S' \subset S\)，\(S' \neq S\)，使得 \(S'\) 是决定性的。

任取 \(h \in S\)。如果 \(S \setminus \{h\}\) 是决定性的，那么我们就得到了结论。因此，假设 \(S \setminus \{h\}\) 不是决定性的。于是，根据第 5 步可知，\(I \setminus (S \setminus \{h\}) = (I \setminus S) \cup \{h\}\) 是决定性的。由第 4 步可知，\(\{h\} = S \cap [(I \setminus S) \cup \{h\}]\) 也是决定性的。因此，我们再次得到了结论，因为根据假设，\(\{h\}\) 是 \(S\) 的一个严格子集。

第 8 步：存在一个 \(h \in I\) 使得 \(S = \{h\}\) 是决定性的。

重复运用第 7 步并且考虑以下两个事实即可得到结论：一个事实是，参与人集合 \(I\) 是有限的；另外一个是根据帕累托性质可知，由所有参与人组成的集合 \(I\) 是决定性的（之前我们已经知道了 \(\emptyset\) 不是）。

第 9 步：如果 \(S \subset I\) 是决定性的，那么对于任何 \(\{x,y\} \subset X\)，\(S\) 完全决定了 \(x\) 比 \(y\) 好。

我们想证明，对于任何 \(T \subset I \setminus S\)，如果 \(S\) 中的每个参与人认为 \(x\) 比 \(y\) 好，\(T\) 中的每个参与人认为 \(x\) 至少与 \(y\) 一样好，而且每个其他参与人认为 \(y\) 比 \(x\) 好，那么社会认为 \(x\) 比 \(y\) 好。为了证明这个性质，取一个不同于 \(x\) 和 \(y\) 的第三个备选方案 \(z \in X\)。根据配对独立性条件可知，我们只要考虑满足下面这样的偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\) 即可，其中

\[\begin{align*} x \succ_i z \succ_i y, \ &\forall i \in S, \\ x \succ_i y \succ_i z, \ &\forall i \in T, \\ y \succ_i z \succ_i x, \ &\forall i \in I \setminus (S \cup T). \end{align*}\]

因为 \(S\) 是决定性的，故有 \(z F_p(\succeq_1, \cdots, \succeq_I) y\)，并且根据第 6 步可知 \(S \cup T\) 是决定性的，故 \(x F_p(\succeq_1, \cdots, \succeq_I) z\)，因此，根据社会偏好的传递性有 \(x F_p(\succeq_1, \cdots, \succeq_I) y\)，这正是我们想证明的。

第 10 步：如果对于某个 \(h \in I\)，\(S = \{h\}\) 是决定性的，那么 \(h\) 是个独裁者。

如果 \(\{h\}\) 是决定性的，那么根据第 9 步，\(\{h\}\) 完全决定了任何 \(x\) 比 \(y\) 好。也就是说，如果偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\) 使得 \(x \succ_h y\)，那么 \(x F_p(\succeq_1, \cdots, \succeq_I) y\)，这意味着 \(h\) 是个独裁者。

第 8 步和第 10 步一起完成了阿罗不可能定理的证明。

可能的结果¶

阿罗不可能定理多少让人不安，但不能因此认为“民主是不可能的”：阿罗不可能定理其实是说，我们不应该期望集体行动具有个人行动那样的一致性。然而，需要注意，在现实中，集体判断和集体决策随处可见。阿罗不可能定理在本质上表明，我们不能忽视制度细节和政治过程程序。例如，假设人们从三个备选方案 \(\{x,y,z\}\) 进行选择。选择方法是多数投票：先对 \(x\) 和 \(y\) 投票，然后对胜出者和 \(z\) 投票。这将产生一个结果，但这个结果取决于投票日程是如何设定的，也就是说，取决于先对谁投票后对谁投票。程序、规则与社会加总之间的这种相关性有着深远意义。现代政治科学非常强调这一点。

在本节，我们不做大的变动，仍保留基本架构。我们考察如果放松阿罗不可能定理的某些要求，我们能在多大程度上摆脱独裁者的结论。我们首先总结一下阿罗不可能定理成立的所有必要的显性和隐性的条件：

备选方案至少为 3 个；
全域定义域：社会福利泛函数 \(F\) 的定义域为 \(\mathcal{R}^I\) 或 \(\mathcal{P}^I\)；
社会理性：也就是说，对于个人偏好的每个可能组合，\(F(\succeq_1, \cdots, \succeq_I)\) 是个理性偏好关系（即，完备的和传递的）；
配对独立性条件；
帕累托性质条件；
不存在独裁关系：不存在参与人 \(h\) 使得在个人偏好的任何组合上，\(h\) 能对任何一对备选方案强制实施自己的严格偏好。

事实上阿罗不可能定理中的六个假设条件，任何一个都不是多余的，其中任何一个条件的缺失我们都可以举出例子导致阿罗不可能定理的结论不成立。在下面的讨论中，我们将考察放松两种条件的结果：一是我们放松加总偏好的理性要求；二是我们在受限制定义域内提出加总问题。特别地，我们将考虑一个限制条件，即单峰偏好（single-peaked preference），这个限制条件在实践中重要而有用。

不完全社会理性¶

假设我们保留帕累托性质和配对独立性条件但允许社会偏好的理性程度小于完全理性。下面的定义 11 描述了理性偏好在两个方面的弱化；

定义 11：拟传递和非循环的偏好关系

假设 \(X\) 上的偏好关系 \(\succeq\) 是反身的和完备的。

如果由 \(\succeq\) 推导出的严格偏好 \(\succ\)（即，\(x \succ y \iff x \succeq y\) 但 \(y \nsucceq x\)）是传递的，那么我们说\(\succeq\) 是拟传递的（quasitransitive）；
如果 \(\succeq\) 在每个有限子集 \(X' \subset X\) 中都有一个最大元素，即 \(\{x \in X' : x \succeq y,\ \forall y \in X'\} \neq \emptyset\)，那么我们说 \(\succeq\) 是非循环的（acyclic）。

我们不难得到如下结论，其中第一条的证明中我们可以看到“循环”这一词的含义：

偏好性质

拟传递的偏好关系是非循环的，但是非循环的偏好关系未必是拟传递的；
理性偏好关系是拟传递的，但拟传递的偏好关系未必是理性的。

偏好性质证明

假设 \(\succ\) 是拟传递的，暂时假设它不是非循环的。于是存在某个有限集 \(X' \subset X\) 使得该集合对于 \(\succeq\) 没有最大元。也就是说，对于每个 \(x \in X'\)，存在某个 \(y \in X'\) 使得 \(y \succ x\)（即，使得 \(y \succeq x\) 但 \(x \nsucceq y\)）。因此，对于任何整数 \(M\)，我们可以找到一个链 \(x^1 \succ x^2 \succ \cdots \succ x^M\)，其中 \(x^m \in X'\) 对于每个 \(m = 1, \cdots, M\)。如果 \(M\) 大于 \(X'\) 的元素（备选方案）数量，那么在这个链中必定存在着重复。比如说 \(x^m = x^{m'}\) 对于 \(m > m'\)。根据拟传递性可知，\(x^{m'} \succ x^m \succ x^{m'}\)，但这是不可能的，因为根据定义，\(\succ\) 是非反身的。因此，\(\succeq\) 必定是非循环的。

非循环的偏好关系未必是拟传递的例子见下面的例 5。
理性偏好关系是拟传递的显然，拟传递的偏好关系未必理性见下面的例 4。

因此，非循环性条件相对更弱。然而需要注意，非循环性对理性的弱化程度没有那么厉害：例如，注意到，康多塞悖论中的社会偏好就已经违背了非循环性。我们不打算详细讨论在这些弱化社会理性条件下将会发生什么样的结果，这样的结果不是非常重要。下面两个例子是说明性的：

例 4：寡头政治的执政集团

令 \(I\) 为参与人集，\(S \subset I\) 是给定的参与人子集，这个子集称为寡头政治的执政集团（oligarchy）（允许 \(S = \{h\}\) 或 \(S = I\) 这些可能性）。给定任何偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{R}^I\)，社会偏好的构建方法如下：给定任何 \(x,y \in X\)，如果至少存在一个 \(h \in S\) 使得 \(x \succ_h y\)，我们说社会认为 \(x\) 至少与 \(y\) 一样好。因此，社会认为 \(x\) 比 \(y\) 严格好当且仅当寡头政治的执政集团中的每个人认为 \(x\) 比 \(y\) 好。

因此，这一社会偏好满足拟传递性是显然的（注意拟传递性的条件）。但是不满足传递性，例如我们考虑两个参与人 \(i,j \in S\)，如果 \(x \sim_i y\)，根据寡头偏好特点可知 \(x \sim y\)，并假设 \(y \sim_j z\)，则有 \(y \sim z\)。但是事实上所有 \(S\) 中的人都可以认为 \(x \succ z\)，这与前面的假设不矛盾，因此 \(x \succ z\) 是可能的，这就违背了传递性。这也是这一选择函数在阿罗不可能定理中唯一一个未能满足的条件（帕累托性质条件和配对独立性条件显然成立）。然而，对于社会加总问题来说，这个解几乎不能令人满意，因为福利泛函数反应迟缓。在一个极端上，如果寡头政治的执政集团仅有一个人，那么他是独裁者。在另外一个极端上，如果执政集团是整个人群（即 \(S = I\)），那么仅当社会所有成员都能达到完全一致的意见时，该社会才能表达严格偏好。

例 5：否决者

假设有两个参与人和三个备选方案 \(\{x,y,z\}\)。于是给定任何偏好组合 \((\succeq_1, \succeq_2)\)，令社会偏好关系为参与人 1 的偏好，但有一个附加条件：参与人 2 有否决权，他能够否决“社会认为 \(x\) 比 \(y\) 好”。具体地说，如果 \(y \succ_2 x\)，那么社会认为 \(y\) 至少与 \(x\) 一样好。总之，对于任何两个备选方案 \(\{v,w\} \subset \{x,y,z\}\)，如果 \(v \succeq_1 w\)，或者 \(v = y, w = x\) 且 \(v \succ_2 w\)，那么社会认为 \(v\) 至少与 \(w\) 一样好。

这样定义的社会偏好是非循环的，这一点不难看到，我们可以分两种情况讨论，第一种是 \(y \nsucc x\)，那么此时的偏好就是 1 的偏好，自然是理性的；第二种是 \(y \succ x\)，此时 \(z\) 的排序完全由 1 决定，也符合非循环性。但是这一偏好不是拟传递的，这也不难看到，我们只需合理利用否决权构造反例：考虑 \(x \succ_1 z\) 且 \(z \succ_1 y\)，那么根据社会偏好的定义，\(x \succ z\)，\(z \succ y\)，但是有可能出现 \(y \succ_2 x\)，这样就有 \(y \succeq x\)，这就违背了拟传递性。

单峰偏好¶

现在我们阐述最重要的一类受限制的定义域条件：单峰偏好。我们将看到，在这个受限的定义域内，非独裁式加总是可能的。事实上，只要施加一个小的约束条件，在这个受限定义域上，配对多数投票将产生一个社会福利泛函数。

定义 12：线性序

备选方案集 \(X\) 上的一个二元关系 \(\geqslant\) 是 \(X\) 上的一个线性序（linear order），如果它是反身的（即，\(x \geqslant x\) 对于每个 \(x \in X\) 成立）、传递的（即，\(x \geqslant y\) 和 \(y \geqslant z\) 意味着 \(x \geqslant z\)）以及全域的（total，即对于任何不同的 \(x,y \in X\)，要么 \(x \geqslant y\)，要么 \(y \geqslant x\)，但不能都成立）。

线性序的最简单例子就是 \(X\) 为实值线的子集（即 \(X \subset \mathbb{R}\)）且 \(\geqslant\) 是实数的“大于或等于”关系。

下面的定义描述了单峰偏好的概念：

定义 13：单峰偏好

理性偏好关系关于 \(X\) 上的线性序 \(\geqslant\) 是单峰的（single peaked），如果存在一个备选方案 \(x \in X\) 使得 \(\succeq\) 在 \(\{y \in X : x \geqslant y\}\) 上关于 \(\geqslant\) 是递增的，而在 \(\{y \in X : y \geqslant x\}\) 上关于 \(\geqslant\) 是递减的。也就是说：

如果 \(x \geqslant z > y\)，那么 \(z \succ y\)；
如果 \(y > z \geqslant x\)，那么 \(z \succ y\)。

用文字表达：存在某个代表着满足程度最高的备选方案 \(x\)，而且随着我们接近这个峰值点，满意程度也在增加（因此，特别地，不可能存在满意程度的任何其他最大值）。

考虑 \(X\) 是实数轴上的开区间的情况，\(\geqslant\) 就是实数域上的大于等于关系，下图以及下面的例子会给读者关于“单峰”的更直观的体会：

例 6：单峰偏好

假设 \(X = [a,b] \subset \mathbb{R}\) 且 \(\geqslant\) 是实数的“大于或等于”关系。于是 \(X\) 上的一个连续偏好关系 \(\succ\) 关于 \(\geqslant\) 是单峰的当且仅当它是严格凸的，也就是，当且仅当，对于每个 \(w \in X\)，当 \(y \succeq w\)，\(z \succeq w\)，\(y \neq z\) 时我们有 \(ay + (1 - \alpha)z > w\)，其中 \(\alpha \in (0,1)\)。

这一充要条件的证明并不困难。首先证明严格凸是充分条件，我们假设 \(x\) 对于 \(\succeq\) 是最大元（良序集一定存在最大元），然后假设 \(x > z > y\)。于是 \(x \succeq y\)，\(y \succeq y\)，\(x \neq y\)，以及 \(z = \alpha x + (1 - \alpha)y\) 对于某个 \(\alpha \in (0,1)\)。因此，根据严格凸性可知 \(z \succ y\)。对称的情况也是类似的，因此充分性得证。必要性事实上根据单峰的几何意义是非常显然的，读者可以自行书写证明。

下面我们定义一个记号，在之后的讨论中是常用的：

定义 14：单峰偏好集族

给定 \(X\) 上的一个线性序 \(\geqslant\)，我们用 \(\mathcal{R}_\geqslant \subset \mathcal{R}\) 表示关于 \(\geqslant\) 是单峰的所有理性偏好关系组成的集族。

给定一个线性序 \(\geqslant\) 和一组参与人 \(I\)，从现在起，我们考虑偏好 \(\mathcal{R}^I_\geqslant\) 的受限制的定义域。这等价于要求所有参与人关于相同的线性序 \(\geqslant\) 都有单峰偏好。假设在定义域 \(\mathcal{R}^I_\geqslant\) 上我们通过配对多数投票定义社会偏好关系。也就是说，给定一个偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{R}^I_\geqslant\) 和任何 \(\{x,y\} \subset X\)，如果认为 \(x\) 严格比 \(y\) 好的参与人数量大于或等于认为 \(y\) 严格比 \(x\) 好的参与人数量，也就是说，如果 \(\# \{i \in I : x \succ_i y\} \geqslant \# \{i \in I : y \succ_i x\}\)，那么我们将这种关系记为 \(x \hat{F}(\succeq_1, \cdots, \succeq_I) y\)，这个式子可以读为“社会认为 \(x\) 至少与 \(y\) 一样好”。

注意到，根据定义可知，对于任何一对备选方案 \(\{x,y\}\)，我们必定有要么 \(x \hat{F}(\succeq_1, \cdots, \succeq_I) y\)，要么 \(y \hat{F}(\succeq_1, \cdots, \succeq_I) x\)。因此，配对多数投票产生了一个完备的社会偏好关系（这个结论对偏好的任何可能定义域都成立）。

在做了如上定义和观察后，我们的目标是：证明在单峰偏好下，我们总能保证由配对多数投票产生的社会偏好有最大元，也就是说，在多数投票规则下，存在着不可能被任何其他方案击败的方案，从而可以避免阿罗不可能定理中独裁者的出现。得到这一结论的方法非常直接，就是找到这个不可击败的方案。为了定义这一方案，我们先定义中间参与人的概念：

定义 15：中间参与人

令 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{R}^I_\geqslant\) 是偏好的一个固定组合，对于每个 \(i \in I\)，我们用 \(x_i\) 表示 \(\succeq_i\) 的最大元（也就是峰值）。我们称参与人 \(h \in I\) 对于偏好组合 \((\succeq_1, \cdots, \succeq_I)\) 是个中间参与人（median agent），如果

\[ \# \{i \in I : x_h \geqslant x_i\} \geqslant \dfrac{I}{2}\ \text{且}\ \# \{i \in I : x_i \geqslant x_h\} \geqslant \dfrac{I}{2} \]

因此中间参与人就是峰值位于所有人峰值中间的参与人。显然中间参与人总是存在的。下图说明了如何确定中间参与人：

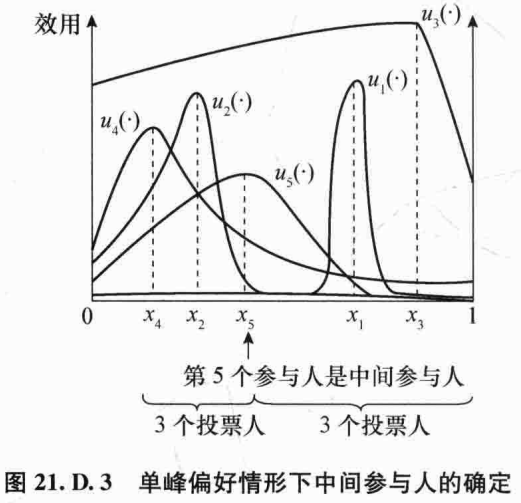
如果峰值不相等而且 \(I\) 是奇数，那么定义 15 表明有 \(\dfrac{I-1}{2}\) 个参与人的峰值严格小于 \(x_h\)，另外 \(\dfrac{I-1}{2}\) 个参与人的峰值严格大于 \(x_h\)。在这种情形下，中间参与人是唯一的。

\(x_h\) 是不可击败的方案

假设 \(\geqslant\) 是 \(X\) 上的一个线性序，考虑偏好组合 \((\succeq_1, \cdots, \succeq_I)\)，在这个偏好组合中，对于每个 \(i\)，\(\succeq_i\) 关于 \(\geqslant\) 是单峰的。令 \(h \in I\) 是个中间参与人。于是 \(x_h \hat{F}(\succeq_1, \cdots, \succeq_I) y\) 对于每个 \(y \in X\) 成立。也就是说，在多数投票下，中间参与人的峰值 \(x_h\) 不可能被任何其他备选方案击败。具有这种性质的任何备选方案称为康多塞获胜者（Condorcet winner）。

因此这一结论表明，只要所有参与人的偏好关于同一个线性序是单峰的，就存在着康多塞获胜者。这一结论也有一个直接推论，就是康多塞悖论中的偏好关系不是单峰的，当然事实上这也是可以直接验证的（因为 \(\{x,y,z\}\) 的 6 种顺序都不能使得三个人的偏好都是单峰的）。

\(x_h\) 是不可击败的方案证明

任取 \(y \in X\) 而且假设 \(x_h > y\)（\(y > x_h\) 的情形的证明类似）。我们需要证明 \(y\) 不能击败 \(x_h\)，也就是说，

\[ \# \{i \in I : x_h \succ_i y\} \geqslant \# \{i \in I : y \succ_i x_h\} \]

考虑参与人集合 \(S \subset I\)，这个集合的峰值大于或等于 \(x_h\)，即，\(S = \{i \in I : x_i \geqslant x_h\}\)。于是 \(x_i \geqslant x_h > y\) 对于每个 \(i \in S\) 成立。因此，根据 \(\succ\) 关于 \(\geqslant\) 的单峰性可知，\(x_h \succ_i y\) 对于每个 \(i \in S\) 成立。另一方面，由于参与人 \(h\) 是个中间参与人，我们有 \(\# S \geqslant \dfrac{I}{2}\)，从而

\[ \# \{i \in I : y \succ_i x_h\} \leqslant \# (I \setminus S) \leqslant \dfrac{I}{2} \leqslant \# S \leqslant \# \{i \in I : x_h \succ_i y\} \]

上面的命题保证了偏好关系 \(\hat{F}(\succeq_1, \cdots, \succeq_I)\) 为非循环的，然而它未必是传递的：

单峰偏好配对多数投票偏好不一定是传递的

我们考虑有三个备选方案 \(\{x,y,z\}\) 的情况，参与人集合 \(I = \{1,2,3,4\}\)，如果四个人的偏好满足

\[\begin{gather*} x \succ_1 y \succ_1 z, \\ z \succ_2 y \succ_2 x, \\ x \succ_3 y \succ_3 z, \\ y \succ_4 z \succ_4 x, \end{gather*}\]

根据多数投票规则，我们有社会认为 \(x \sim y, y \succ z, z \sim x\)。这就违背了传递性。

事实上，偏好关系 \(\hat{F}(\succeq_1, \cdots, \succeq_I)\) 在下列这种特殊情形下是传递的：当 \(I\) 为奇数时；而且对于每个 \(i\)，偏好关系 \(\succeq_i\) 属于集族 \(\mathcal{P}_\geqslant \subset \mathcal{R}_\geqslant\)，其中 \(\geqslant\) 是由具有下列两个性质的偏好关系 \(\succeq\) 组成的：

\(\succeq\) 关于 \(\geqslant\) 是单峰的；
对于 \(\succeq\)，不存在无差异的两个不同备选方案。

注意到，如果 \(I\) 为奇数而且偏好属于 \(\mathcal{P}_\geqslant\)，那么对于任何一对备选方案，在多数投票规则下，一个方案总是严格好于另外一个。因此，在这种情形下，一个康多塞获胜方案总能击败任何其他备选方案。

配对多数投票产生的社会偏好是理性的条件

假设 \(I\) 是奇数，而且 \(\geqslant\) 是 \(X\) 上的一个线性序。于是配对多数投票产生了一个良好定义的社会福利泛函数 \(F : \mathcal{P}^I_\geqslant \to \mathcal{R}\)。也就是说，如果偏好定义域关于 \(\geqslant\) 是单峰的，而且在该定义域不存在无差异的两个不同备选方案，那么我们可以断言由配对多数投票产生的社会偏好关系 \(\hat{F}(\succeq_1, \cdots, \succeq_I)\) 是完备的和传递的。

配对多数投票产生的社会偏好是理性的条件证明

我们已经知道 \(\hat{F}(\succeq_1, \cdots, \succeq_I)\) 是完备的，因为任何两个备选方案都可以通过多数投票规则进行比较，因此剩下的任务是证明它是传递的。假设 \(x \hat{F}(\succeq_1, \cdots, \succeq_I) y\) 和 \(y \hat{F}(\succeq_1, \cdots, \succeq_I) z\)。在我们的假设条件下（回忆 \(I\) 是奇数而且任何个人对于方案都不允许无差异），\(x\) 击败了 \(y\)，\(y\) 击败了 \(z\)（奇数且非无差异投票不可能出现平局）。考虑集合 \(X' = \{x,y,z\}\)，如果偏好被限制在这个集合上，那么相对于 \(X'\)，偏好仍然属于 \(\mathcal{P}_\geqslant\)，因此 \(X'\) 中存在着一个备选方案，它不可能被 \(X'\) 中的任何其他备选方案击败。这个备选方案不是 \(y\)（因为 \(y\) 被 \(x\) 击败），也不是 \(z\)（因为 \(z\) 被 \(y\) 击败）。因此，它必定是 \(x\)，我们断言 \(x \hat{F}(\succeq_1, \cdots, \succeq_I) z\)，这样就证明了传递性。

这样我们就结束了两个角度放松阿罗不可能定理前提从而避免独裁社会选择函数的讨论：一方面我们可以放松社会理性的假设，我们可以得到寡头政治、否决者等非独裁的社会决策模型；另一方面我们可以限制偏好的定义域为单峰偏好，得到在多数投票规则下，中间投票人的峰值是不可击败的结论，并且多数投票在上面定理的前提下导出的社会偏好也是理性的。

除此之外，在 MWG《微观经济理论》21.D 节最后的小字部分还讨论了备选方案落在多维空间的一些复杂情况，感兴趣的读者可以自行阅读，从此不再赘述。

社会选择函数¶

在前面几节我们完成的任务是如何将个人偏好关系组合加总为一致的（即，理性的）社会偏好序。然后，这个社会偏好序可能被用作决策依据。在本节，我们直接考察社会决策，将社会加总问题视为分析个人偏好组合如何转变为社会决策的问题。我们得到的主要结果再一次地产生了独裁者结论。在某种意义上，这个结果等价于将阿罗不可能定理翻译为选择函数的语言。它也起到了重新解释配对独立性条件的作用，为本章内容和机制设计中基于激励的分析提供了联系。

与以前一样，我们有一组备选方案 \(X\) 和一组有限个参与人 \(I\)。\(X\) 上的偏好关系 \(\succeq\) 构成的集合记为 \(\mathcal{R}\)。我们将在 \(\mathcal{R}\) 中由满足任何两个不同方案对于 \(\succeq\) 都不是无差异这一性质的偏好关系组成的子集记为 \(\mathcal{P}\)。

定义 16：社会选择函数

给定任何子集 \(\mathcal{A} \subset \mathcal{R}^I\)，定义在 \(X\) 上的一个社会选择函数（social choice function） \(f : \mathcal{A} \to X\)，对每个 \(\succeq_1, \cdots, \succeq_I \in \mathcal{A}\) 都指定了一个选定的元素 \(f(\succeq_1, \cdots, \succeq_I) \in X\)。

社会选择函数的概念蕴含着一个要求：选择集是单值的，当然某些情况下我们也允许选择集是多值的，当然单值想强调的是要求参与人的选择不是随机的。

如果 \(X\) 是有限的，定义域上的每个社会福利函数 \(F\) 产生了一个自然的社会选择函数：对于每个 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\) 指定了 \(X\) 中关于社会偏好关系 \(F(\succeq_1, \cdots, \succeq_I)\) 而言的一个最受偏好的元素。例如，如果与之前保证配对多数投票产生的社会偏好是理性的情形一样，\(\mathcal{A} \subset \mathcal{P}_\geqslant^I\) 是单峰偏好的定义域，\(I\) 为奇数，\(F\) 是定义在 \(\mathcal{A}\) 上的配对多数投票社会福利泛函数，那么对于每个 \((\succeq_1, \cdots, \succeq_I)\)，\(f(\succeq_1, \cdots, \succeq_I)\) 这个选择是 \(X\) 中的康多塞获胜方案。

现在我们阐述和证明一个类似于阿罗不可能定理的结果。回忆对于阿罗不可能定理，我们有两个条件：社会福利泛函数必须具有帕累托性质，而且必须是配对独立的。此处我们再次要求两个条件：首先，社会选择函数必须再次具有（弱）帕累托性质；其次，这个函数必须是单调的。下面的两个定义分别给出了这两个概念：

定义 17：帕累托性质

定义在 \(\mathcal{A} \subset \mathcal{R}^I\) 上的社会选择函数 \(f : \mathcal{A} \to X\) 是弱帕累托的（weakly Paretian），如果对于任何偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\)，\(f(\succeq_1, \cdots, \succeq_I) \in X\) 这个选择是弱帕累托最优的，也就是说，如果对于某对方案 \(\{x,y\} \subset X\) 我们有 \(x \succ_i y\) 对于每个 \(i\) 成立，那么 \(y \neq f(\succeq_1, \cdots, \succeq_I)\)。

这个概念非常自然，就是说如果所有人都认为 \(x\) 比 \(y\) 好，那么 \(y\) 一定不可能是最后的社会选择。接下来我们定义单调性，为了定义单调性，我们需要一个更基础的概念：

定义 18：位置保留

备选方案 \(x \in X\) 将它在组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{R}^I\) 中的位置（position）保留到了 \((\succeq_1', \cdots, \succeq_I') \in \mathcal{R}^I\)，如果

\[ x \succeq_i y\ \text{意味着}\ x \succeq_i' y \]

对于每个 \(i\) 和每个 \(y \in X\) 成立。

用文字表示，\(x\) 将自己在 \((\succeq_1, \cdots, \succeq_I)\) 中的位置保留到了 \((\succeq_1', \cdots, \succeq_I')\)，如果从 \(\succeq_i\) 变为 \(\succeq_i'\) 时，对于每个 \(i\)，劣于（或无差异于） \(x\) 的备选方案集扩大了（或维持不变）。也就是说，下轮廓集

\[ L(x,\succeq_i) = \{y \in X : x \succeq_i y\} \subset L(x,\succeq_i') = \{y \in X : x \succeq_i' y\} \]

注意，定义 18 中的条件没有要求从 \(\succeq_i\) 变为 \(\succeq_i'\) 时其它备选方案如何改变它们相互之间的位置。

定义 19：单调性

定义在 \(\mathcal{A} \subset \mathcal{R}^I\) 上的社会选择函数 \(f : \mathcal{A} \to X\) 是单调的（monotonic），如果对于任何两个组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\) 和 \((\succeq_1', \cdots, \succeq_I') \in \mathcal{A}\)，如果备选方案 \(x = f(\succeq_1, \cdots, \succeq_I)\) 将它在 \((\succeq_1, \cdots, \succeq_I)\) 中的位置保留到了 \((\succeq_1', \cdots, \succeq_I')\)，那么我们有 \(f(\succeq_1', \cdots, \succeq_I') = x\)。

用文字表达：如果任何一个备选方案都不能从选择集中删除，除非某个参与人喜欢它的程度下降了（它的位次向后移动了），那么选择函数是单调的。实际上这很容易让我们回忆起社会福利泛函数的正反应性。

是否存在同时满足弱帕累托性和单调性的社会选择函数？答案是肯定的，事实上读者不难验证：定义在单峰偏好定义域上的配对多数投票社会决策函数是弱帕累托的和单调的。但是如果我们的定义域是全域（即 \(\mathcal{A} = \mathcal{R}^I\) 或 \(\mathcal{A} = \mathcal{P}^I\)），结果又是怎样的？在这个定义域上存在着具有这两个性质的一类社会选择函数，它们就是我们不怎么喜欢的独裁社会选择函数。

定义 20：独裁社会选择函数

参与人 \(h \in I\) 对于社会选择函数 \(f : \mathcal{A} \to X\) 来说是个独裁者，如果对于每个组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\)，在 \(X\) 中 \(f(\succeq_1, \cdots, \succeq_I)\) 对于 \(\succeq_h\) 都是最受偏好的选择；也就是说，

\[ f(\succeq_1, \cdots, \succeq_I) \in \{x \in X : x \succeq y\ \text{对于每个}\ y \in X\} \]

允许存在独裁者的社会选择函数称为独裁的（dictatorial）社会选择函数。

用更通俗的语言描述，即在任何偏好组合下，社会选择的都是独裁者 \(h\) 最偏好的结果。显然的事情是，在定义域中，一个独裁的社会选择函数是弱帕累托的和单调的。遗憾的是，在全域定义域（即 \(\mathcal{A} = \mathcal{R}^I\) 或 \(\mathcal{A} = \mathcal{P}^I\)）中，最好的结果就是独裁的社会选择函数：

阿罗不可能定理在社会选择函数下的推论

假设备选方案的数量至少有三个，可行偏好组合的定义域为 \(\mathcal{A} = \mathcal{R}^I\) 或 \(\mathcal{A} = \mathcal{P}^I\)。那么每个弱帕累托的和单调的社会选择函数 \(f : \mathcal{A} \to X\) 是独裁的。

这个结果的证明可以作为阿罗不可能定理的一个推论。为了完成此事，我们要推导出一个社会福利泛函数 \(F\)，它能将 \(f(\succeq_1, \cdots, \succeq_I)\) 对于每个组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\) 理性化。然后证明 \(F\) 满足阿罗不可能定理的假设条件，从而得到了独裁关系结论。其中最关键的步骤就是从社会选择函数 \(f\) 导出福利函数 \(F\)，这需要我们下面的定义：

定义 21：置顶

给定一个有限子集 \(X' \subset X\) 和一个组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{R}^I\)，我们说组合 \((\succeq_1', \cdots, \succeq_I')\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中把 \(X'\) 置顶（takes \(X'\) to the top），如果对于每个 \(i\)，

\[\begin{gather*} x \succ_i' y\ \text{对于每个}\ x \in X\ \text{和}\ y \notin X' \\ x \succeq_i y \iff x \succeq_i' y\ \text{对于每个}\ x,y \in X' \end{gather*}\]

用文字表达：\(\succeq_i'\) 是通过下列方法得到的——在 \(\succeq_i\) 中把 \(X'\) 中的每个备选方案的位置都向最前方移动，但保留 \(X'\) 中的这些备选方案之间（弱或严格的）次序不变。\(X'\) 之外的备选方案之间的次序则是任意的。例如，如果 \(x \succ_i y \succ_i z \succ_i w\)，那么由 \(y \succ_i' w \succ_i' z \succ_i' x\) 定义的偏好关系 \(\succeq_i'\) 把 \(\{y,w\}\) 从 \(\succeq_i\) 中置顶。还要注意，如果 \((\succeq_1', \cdots, \succeq_I')\) 将 \(X'\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中置顶，那么每个 \(x \in X'\) 将它在 \((\succeq_1, \cdots, \succeq_I)\) 中的位置保留到了 \((\succeq_1', \cdots, \succeq_I')\)。

余下的证明我们分若干步骤进行：

独裁社会选择函数证明

第 1 步：如果组合 \((\succeq_1', \cdots, \succeq_I') \in \mathcal{A}\) 和 \((\succeq_1'', \cdots, \succeq_I'') \in \mathcal{A}\) 都把 \(X' \subset X\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中置顶，那么 \(f(\succeq_1', \cdots, \succeq_I') = f(\succeq_1'', \cdots, \succeq_I'')\)。

这一步是显然的，首先利用弱帕累托性质可知 \(f(\succeq_1', \cdots, \succeq_I') \in X'\)，然后利用单调性质可知 \(f(\succeq_1', \cdots, \succeq_I') = f(\succeq_1'', \cdots, \succeq_I'')\)（因为置顶过程 \(X'\) 位置保留）。

第 2 步：定义 \(F(\succeq_1, \cdots, \succeq_I)\)。

对于每个组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\)，我们定义 \(X\) 上的一个二元关系 \(F(\succeq_1, \cdots, \succeq_I)\)。具体地说，我们令 \(x F(\succeq_1, \cdots, \succeq_I) y\)（读作“社会认为 \(x\) 至少与 \(y\) 一样好”），如果 \(x = y\) 或 \(x = f(\succeq_1', \cdots, \succeq_I')\) 当 \((\succeq_1', \cdots, \succeq_I') \in \mathcal{A}\) 是把 \(\{x,y\}\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中置顶的任何偏好组合时。根据第 1 步，这个二元关系是良定义的，也就是说，与我们选择的特定偏好组合 \((\succeq_1', \cdots, \succeq_I')\) 无关。

第 3 步：对于每个组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\)，\(F(\succeq_1, \cdots, \succeq_I)\) 是个理性偏好关系。而且，\(F(\succeq_1, \cdots, \succeq_I) \in \mathcal{P}\)，也就是说，对于两个不同备选方案，社会不会认为它们是无差异的。

由 \(f\) 的弱帕累托性质可知，当 \((\succeq_1', \cdots, \succeq_I')\) 把 \(\{x,y\}\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中置顶时，我们有 \(f(\succeq_1', \cdots, \succeq_I') \in \{x,y\}\)。因此，我们断言：要么 \(x F(\succeq_1, \cdots, \succeq_I) y\)，要么 \(y F(\succeq_1, \cdots, \succeq_I) x\)，但不可能都成立（除非 \(x = y\)），不可能都成立的原因是第 1 步保证了 \(f\) 取值唯一性。特别地，\(F(\succeq_1, \cdots, \succeq_I)\) 是完备的。

为了验证传递性，假设 \(x F(\succeq_1, \cdots, \succeq_I) y\) 和 \(y F(\succeq_1, \cdots, \succeq_I) z\)。我们假设这三个备选方案 \(\{x,y,z\}\) 是不同的。令 \((\succeq_1'', \cdots, \succeq_I'') \in \mathcal{A}\) 是个把 \(\{x,y,z\}\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中置顶的偏好组合。由于 \(f\) 是弱帕累托的，我们有 \(f(\succeq_1'', \cdots, \succeq_I'') \in \{x,y,z\}\)。

假设我们有 \(y = f(\succeq_1', \cdots, \succeq_I')\)。考虑一个把 \(\{x,y\}\) 从 \((\succeq_1'', \cdots, \succeq_I'')\) 中置顶的偏好组合 \((\succeq_1', \cdots, \succeq_I') \in \mathcal{A}\)。由于 \(y\) 把它在 \((\succeq_1'', \cdots, \succeq_I'')\) 中的位置保留到了 \((\succeq_1', \cdots, \succeq_I')\)，由单调性可知，\(f(\succeq_1', \cdots, \succeq_I') = y\)。但是 \((\succeq_1', \cdots, \succeq_I')\) 也将 \(\{x,y\}\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中置顶：当从 \((\succeq_1, \cdots, \succeq_I)\) 到 \((\succeq_1', \cdots, \succeq_I')\) 时，在任何个人偏好关系中，\(x\) 和 \(y\) 的相对位置（它们是排在最前端的两个备选方案）都未发生变化。因此，我们断言 \(y F(\succeq_1, \cdots, \succeq_I) x\)，这违背了 \(x F(\succeq_1, \cdots, \succeq_I) y, x \neq y\) 这个假设。因此， \(y \neq f(\succeq_1'', \cdots, \succeq_I'')\)。

类似地，我们得到 \(z \neq f(\succeq_1'', \cdots, \succeq_I'')\)。我们仅需要使用 \(\{y,z\}\) 来重复相同的论证即可。剩下的唯一可能是 \(x = f(\succeq_1'', \cdots, \succeq_I'')\)。因此，令 \((\succeq_1', \cdots, \succeq_I') \in \mathcal{A}\) 把 \(\{x,z\}\) 从 \((\succeq_1'', \cdots, \succeq_I'')\) 中置顶。由于 \(x\) 将它在 \((\succeq_1'', \cdots, \succeq_I'')\) 中的位置保留到了 \((\succeq_1', \cdots, \succeq_I')\)，所以 \(x = f(\succeq_1', \cdots, \succeq_I')\)。但是 \((\succeq_1', \cdots, \succeq_I')\) 也把 \(\{x,z\}\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中置顶。因此，\(x F(\succeq_1, \cdots, \succeq_I) z\)。这样我们就证明了传递性。

第 4 步：社会福利泛函数 \(F : \mathcal{A} \to \mathcal{P}\) 理性化了社会选择函数 \(f : \mathcal{A} \to X\)；也就是说，对于每个组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\)，\(f(\succeq_1, \cdots, \succeq_I)\) 在 \(X\) 中对于 \(F(\succeq_1, \cdots, \succeq_I)\) 是最受偏好的备选方案。

这个结论非常直观，因为 \(F\) 是由 \(f\) 构建出的。记 \(x = f(\succeq_1, \cdots, \succeq_I)\)，令 \(y \neq x\) 为任何其他备选方案。考虑偏好组合 \((\succeq_1', \cdots, \succeq_I') \in \mathcal{A}\)，它将 \(\{x,y\}\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中置顶。由于 \(x\) 把它在 \((\succeq_1, \cdots, \succeq_I)\) 中的位置保留到了 \((\succeq_1', \cdots, \succeq_I')\)，我们有 \(x = f(\succeq_1', \cdots, \succeq_I')\)。因此根据第 2 步 \(F\) 的定义，我们有 \(x F(\succeq_1, \cdots, \succeq_I) y\)。

第 5 步：社会福利泛函数 \(F : \mathcal{A} \to \mathcal{P}\) 是帕累托的。

显然，如果 \(x \succ_i y\) 对于每个 \(i\) 成立，那么根据 \(f\) 的帕累托性质，当 \((\succeq_1', \cdots, \succeq_I')\) 把 \(\{x,y\}\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中置顶时，我们必定有 \(x = f(\succeq_1', \cdots, \succeq_I')\)。因此，\(x F(\succeq_1, \cdots, \succeq_I) y\)，根据第 3 步可知，\(x F_p(\succeq_1, \cdots, \succeq_I) y\)。

第 6 步：社会福利泛函数 \(F : \mathcal{A} \to \mathcal{P}\) 满足配对独立性条件。

假设在 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{A}\) 和 \((\succeq_1', \cdots, \succeq_I') \in \mathcal{A}\) 中，对于每个 \(i\)，\(\{x,y\}\) 的位置是相同的（也就是说，对于每个 \(i\)，\(x \succeq_i y\) 当且仅当 \(x \succeq_i' y\)）。假设 \((\succeq_1'', \cdots, \succeq_I'')\) 将 \(\{x,y\}\) 从 \((\succeq_1, \cdots, \succeq_I)\) 中置顶，而且比如 \(x = f(\succeq_1'', \cdots, \succeq_I'')\)。于是 \(x F(\succeq_1, \cdots, \succeq_I) y\)。但是 \((\succeq_1'', \cdots, \succeq_I'')\) 也将 \(\{x,y\}\) 从 \((\succeq_1', \cdots, \succeq_I')\) 中置顶。因此 \(x F(\succeq_1', \cdots, \succeq_I') y\)，这正是我们想证明的。

第 7 步：社会选择函数 \(f : \mathcal{A} \to X\) 是独裁的。

根据阿罗不可能定理以及之前的 4、5、6 步可以立即得到（第 4 步的意义就是保证 \(f\) 取出的是独裁者最偏好的方案）。

在本讲的最后，我们来讨论一下下列推论，它表明上面的定理和如实显示偏好的激励问题相关，我们将在机制设计中详细分析后面这个问题：

独裁社会选择函数的推论

假设备选方案至少有三个，\(f : \mathcal{P}^I \to X\) 是个社会选择函数，它具有弱帕累托性质且满足下列无谎报的激励（no-incentive-to-misrepresent）条件：

\[ f(\succeq_1, \cdots, \succeq_{h-1}, \succ_h, \succeq_{h+1}, \cdots, \succeq_I) \succeq_h f(\succeq_1, \cdots, \succeq_{h-1}, \succeq_h', \succeq_{h+1}, \cdots, \succeq_I) \]

对于每个参与人 \(h\)、每个 \(\succeq_h' \in \mathcal{P}\) 和每个偏好组合 \((\succeq_1, \cdots, \succeq_I) \in \mathcal{P}^I\) 成立。那么 \(f\) 是独裁的。

推论的证明

根据前面的定理可知，我们只需证明 \(f\) 是单调的即可。假设它不是单调的。不失一般性，我们假设对于某个参与人 \(h\)，存在参与人 \(i \neq h\) 的偏好 \(\succeq_i \in \mathcal{P}\) 以及参与人 \(h\) 的偏好 \(\succeq_h'', \succeq_h''' \in \mathcal{P}\)，使得

\[\begin{gather*} x = f(\succeq_1, \cdots, \succeq_{h-1}, \succeq_h'', \succeq_{h+1}, \cdots, \succeq_I) \\ y = f(\succeq_1, \cdots, \succeq_{h-1}, \succeq_h''', \succeq_{h+1}, \cdots, \succeq_I) \end{gather*}\]

并且我们有 \(x \succeq_h'' z\) 意味着 \(x \succeq_h''' z\) 对于每个 \(z \in X\) 成立，但 \(y \neq x\)（也就是说 \(x\) 的位置保留了，但选择发生了变化）。那么我们有两种可能性：要么 \(y \succ_h'' x\)，要么 \(x \succeq_h'' y\)。

如果 \(y \succ_h'' x\)，那么无谎报的激励条件不成立，因为如果我们考虑如下情况：“真实的”偏好关系为 \(\succeq_h = \succeq_h''\)，谎报的偏好关系为 \(\succeq_h' = \succeq_h'''\)；
如果 \(x \succeq_h'' y\)，那么 \(x \succeq_h''' y\)。因此，由于不存在两个无差异的不同方案，所以 \(x \succ_h''' y\)。但是如果 \(x \succ_h''' y\)，那么无谎报的激励条件不成立，因为如果我们考虑如下情况：“真实的”偏好关系为 \(\succeq_h = \succeq_h'''\)，谎报的偏好关系为 \(\succeq_h' = \succeq_h''\)。

事实上这里的证明和结论能让我们想起迈尔森引理（见机制设计的最优机制一节）中诚实报价与单调性之间的关系。事实上，只要不满足单调性，我们总能找到一些反例使得不诚实报价可以获得更好的结果。