占优策略的执行¶

基本定义¶

不完全信息下占优策略的基本定义¶

在上一讲简介中，我们引出了机制设计的核心问题：什么样的社会选择函数是可以被执行的。我们引入了显示原理，它表明在占优策略均衡或贝叶斯纳什均衡的情形下，可以被执行的社会选择函数必定是可以被如实执行的，因此我们只需要把目光放在激励相容的直接显示机制上即可。在本讲，我们首先研究占优策略中的执行问题，下一讲将讨论贝叶斯纳什均衡下的执行问题。

我们始终使用此前简介中引入的符号：参与人类型向量 \(\theta = (\theta_1, \cdots, \theta_I)\) 是根据概率密度 \(\phi\) 从集合 \(\Theta = \Theta_1 \times \cdots \times \Theta_I\) 中抽取出的；给定参与人 \(i\) 的类型 \(\theta_i\)，他在备选方案 \(X\) 上的伯努利效用函数为 \(u_i(x, \theta_i)\)。另外，为简单起见，我们记 \(\theta_{-i} = (\theta_1, \cdots, \theta_{i-1}, \theta_{i+1}, \cdots, \theta_I)\) 且 \(\theta = (\theta_i, \theta_{-i})\)。机制 \(\Gamma = (S_1, \cdots, S_I, g(\cdot))\) 是由 \(I\) 个策略集 \(S_1, \cdots, S_I\) 和一个结果函数 \(g: S \to X\) 组成的一个集族，其中，每个 \(S_i\) 包含参与人 \(i\) 的可能行动（或行动计划）；\(S = S_1 \times \cdots \times S_I\)。与此前讨论的一致，机制 \(\Gamma = (S_1, \cdots, S_I, g(\cdot))\)、可能的类型 \((\Theta, \cdots, \Theta_I)\)、概率密度 \(\phi\) 以及伯努利效用函数 \((u_1(\cdot), \cdots, u_I(\cdot))\) 定义了一个不完全信息博弈。另外，我们记 \(s_{-i} = (s_1, \cdots, s_{i-1}, s_{i+1}, \cdots, s_I)\)，\(s = (s_i, s_{-i})\)，以及 \(S_{-i} = S_1 \times \cdots \times S_{i-1} \times S_{i+1} \times \cdots \times S_I\)。

在博弈论基础中我们就已经知道，对于博弈中的参与人 \(i\) 的某个策略来说，无论 \(i\) 的竞争对手选择哪个可能策略，\(i\) 的这个策略带给他的收益都不小于他的任何其他可能策略带来的收益，那么这个策略是参与人 \(i\) 的一个弱占优策略。在当前的非完全信息环境下，对于参与人 \(i\) 来说，策略 \(s_i: \Theta_i \to S_i\) 是他在机制 \(\Gamma = (S_1, \cdots, S_I, g(\cdot))\) 中的一个弱占优策略，如果对于所有 \(\theta_i \in \Theta_i\) 和参与人 \(j \neq i\) 的所有可能策略 \(s_{-i}(\cdot) = (s_1(\cdot), \cdots, s_{i-1}(\cdot), s_{i+1}(\cdot), \cdots, s_I(\cdot))\)，我们有

\[ E_{\theta_{-i}}[u_i(g(s_i(\theta_i), s_{-i}(\theta_{-i})), \theta_i) \mid \theta_i] \geqslant E_{\theta_{-i}}[u_i(g(s_i', s_{-i}(\theta_{-i})), \theta_i) \mid \theta_i],\ \forall s_i' \in S_i \tag{1} \label{mech-dom-1} \]

关于这一表达式，需要强调以下几点：

这里的期望针对的是 \(\theta_{-i}\) 的不确定性；
不等号右侧 \(s_i'\) 不再是 \(\theta_i\) 的函数，可以是一个固定的行动，这是因为对于 \(i\) 而言 \(\theta_i\) 是一个已知的值，所以直接固定行动也是可以的，但等号左边的 \(s_i\) 仍然是 \(\theta_i\) 的函数，因为我们要求对于任意的 \(\theta_i\) 占优策略都满足这一条件，我们需要为任意的 \(\theta_i\) 值设计相应的策略。

事实上这一定义非常容易理解，与完全信息条件下的仅仅是多了一层条件期望。但是这一条件验证起来显然更加复杂，幸运的是，我们有如下结论可以对上面的条件进行简化：

占优策略的等价定义

占优策略的定义式 \(\eqref{mech-dom-1}\) 等价于

\[ u_i(g(s_i(\theta_i),s_{-i}),\theta_i) \geqslant u_i(g(s_i',s_{-i}),\theta_i),\ \forall s_i' \in S_i,s_{-i} \in S_{-i},\theta_i \in \Theta_i \tag{2} \label{mech-dom-2} \]

占优策略等价定义的证明

\(\eqref{mech-dom-1} \implies \eqref{mech-dom-2}\)：显然，我们只需在 \(\eqref{mech-dom-1}\) 中取 \(s_{-i}(\theta_{-i}) = s_{-i}\) 即可（即取与 \(\theta_{-i}\) 无关的固定策略 \(s_{-i}\)）；
\(\eqref{mech-dom-2} \implies \eqref{mech-dom-1}\)：事实上，\(s_{-i}(\theta_{-i})\) 在 \(\theta_{-i}\) 固定的时候就是一个固定策略 \(s_{-i}\)，因此这一个方向证明的核心就是把 \(\eqref{mech-dom-2}\) 视为不同的 \(\theta_{-i}\) 下不同的 \(s_{-i}\) 的情况，然后以条件概率 \(p(\cdot \mid \theta_i)\) 求期望即可推出 \(\eqref{mech-dom-1}\)。形式化地表达就是，由 \(\eqref{mech-dom-2}\) 可得

\[ \sum\limits_{\theta_{-i}} p(\theta_{-i} \mid \theta_i) u_i(g(s_i(\theta_i),s_{-i}),\theta_i) \geqslant \sum\limits_{\theta_{-i}} p(\theta_{-i} \mid \theta_i) u_i(g(s_i',s_{-i}),\theta_i),\ \forall s_i' \in S_i \]

对任意的 \(\theta_i\) 和 \(s_{-i}\) 都成立。如果我们将 \(\eqref{mech-dom-1}\) 展开，事实上也会得到这一表达式，从而证明了 \(\eqref{mech-dom-1}\)（甚至我们可以直接通过这一观察证明 \(\eqref{mech-dom-1} \iff \eqref{mech-dom-2}\)）。

总而言之，上面的讨论可以引出下面的定义 1：

定义 1：占优策略

策略组合 \(s^*(\cdot) = (s_1^*(\cdot), \cdots, s_I^*(\cdot))\) 是机制 \(\Gamma = (S_1, \cdots, S_I, g(\cdot))\) 的一个占优策略均衡，如果对于所有 \(i\) 和所有 \(\theta_i \in \Theta_i\)，我们有

\[ u_i(g(s_i^*(\theta_i), s_{-i}), \theta_i) \geqslant u_i(g(s_i, s_{-i}), \theta_i) \]

对于所有 \(s_i \in S_i\) 和所有 \(s_{-i} \in S_{-i}\) 成立。

有了这一定义后，我们也能迁移上一讲中执行的定义到占优策略均衡的情形，这里不再赘述。我们对占优策略执行特别感兴趣，这是因为如果我们占优执行的机制是非常强和稳健的。因为在博弈论中我们就知道占优策略是最强、对理性假设最弱的解概念。除此之外，根据 \(\eqref{mech-dom-2}\) 可知，占优策略不需要先验概率分布就可以判断，因此即使我们不知道参与人的类型分布，也可以判断一个策略是否是占优的。

显示原理的讨论¶

给出基本定义后，回到我们的核心问题，即什么样的社会选择函数是可执行的。在上一讲中我们已经讨论过，为了识别某个特定社会选择函数 \(f\) 是否为可执行的，显示原理告诉我们只需要识别那些能被如实执行的社会选择函数即可。迁移之前激励相容的概念以及占优的等价定义，我们给出下面的定义：

定义 2：占优策略激励相容

社会选择函数 \(f\) 在占优策略中是如实可执行的（truthfully implementable in dominant strategies）或占优策略激励相容的（dominant strategy incentive compatible）或防策略的（strategy-proof）或直观的（straightforward），如果 \(s_i^*(\theta_i) = \theta_i\) 对于所有 \(\theta_i \in \Theta_i\) 和所有 \(i\) 是直接显示机制 \(\Gamma = (\Theta_1, \cdots, \Theta_I, f(\cdot))\) 的一个占优策略均衡。也就是说，如果对于所有 \(i\) 和所有 \(\theta_i \in \Theta_i\)，我们有

\[ u_i(f(\theta_i, \theta_{-i}), \theta_i) \geqslant u_i(f(\theta_i', \theta_{-i}), \theta_i) \tag{3} \label{mech-dom-3} \]

对于所有 \(\theta_i' \in \Theta\) 和所有 \(\theta_{-i} \in \Theta_{-i}\) 成立。

因此根据显示原理，在理论上，为了识别某个特定社会选择函数 \(f\) 是否为占优策略可执行的，我们只要检验不等式 \(\eqref{mech-dom-3}\) 即可。

鉴于不等式 \(\eqref{mech-dom-3}\) 是社会选择函数 \(f\) 能在占优策略中被如实执行的必要且充分条件，我们可以将其解释为某种弱偏好逆转性质（weak preference reversal property）：考虑任何参与人 \(i\)，以及参与人 \(i\) 的任何一对可能类型 \(\theta_i'\) 和 \(\theta_i''\)。如果如实报告是参与人 \(i\) 的一个占优策略，那么对于任何 \(\theta_{-i} \in \Theta_{-i}\)，我们必定有

\[ u_i(g(f(\theta_i', \theta_{-i}), \theta_i')) \geqslant u_i(g(f(\theta_i'', \theta_{-i}), \theta_i')) \]

和

\[ u_i(g(f(\theta_i'', \theta_{-i}), \theta_i'')) \geqslant u_i(g(f(\theta_i', \theta_{-i}), \theta_i'')) \]

也就是说，当参与人 \(i\) 的类型从 \(\theta_i'\) 变为 \(\theta_i''\) 时，他对 \(f(\theta_i', \theta_{-i})\) 和 \(f(\theta_i'', \theta_{-i})\) 的偏好排序必定是弱逆转的（weakly reverse）：当他的类型为 \(\theta_i'\) 时，他偏好 \(f(\theta_i', \theta_{-i})\) 弱胜于 \(f(\theta_i'', \theta_{-i})\)；当他的类型为 \(\theta_i''\) 时，他偏好 \(f(\theta_i'', \theta_{-i})\) 弱胜于 \(f(\theta_i', \theta_{-i})\)。事实上，我们还可以证明一个反方向的结论，即如果这个弱偏好逆转性质对于所有 \(\theta_{-i} \in \Theta_{-i}\) 和所有组合 \(\theta_i', \theta_i'' \in \Theta_i\) 成立，那么如实报告的确是参与人 \(i\) 的一个占优策略。

如果使用参与人 \(i\) 的下轮廓集（lower contour sets），我们能更简洁地表达这个弱偏好逆转性质。我们把参与人 \(i\) 的类型为 \(\theta_i\) 时他的备选方案 \(x\) 的下轮廓集定义为

\[ L_i(x, \theta_i) = \{ z \in X \mid u_i(x, \theta_i) \geqslant u_i(z, \theta_i) \} \]

有了这个下轮廓集之后，我们就能更简洁地刻画可在占优策略中如实执行的社会选择函数集：

占优策略激励相容的另一种刻画

社会选择函数 \(f\) 是可在占优策略中如实执行的，当且仅当对于所有参与人 \(i\)、所有 \(\theta_{-i} \in \Theta_{-i}\) 以及参与人 \(i\) 的所有类型组合 \(\theta_i', \theta_i'' \in \Theta_i\)，我们有

\[ f(\theta_i', \theta_{-i}) \in L_i(f(\theta_i'', \theta_{-i}), \theta_i'')\ \text{和 } f(\theta_i'', \theta_{-i}) \in L_i(f(\theta_i', \theta_{-i}), \theta_i') \]

对于可在占优策略中如实执行的社会选择函数的偏好逆转特征，我们可用下图说明：

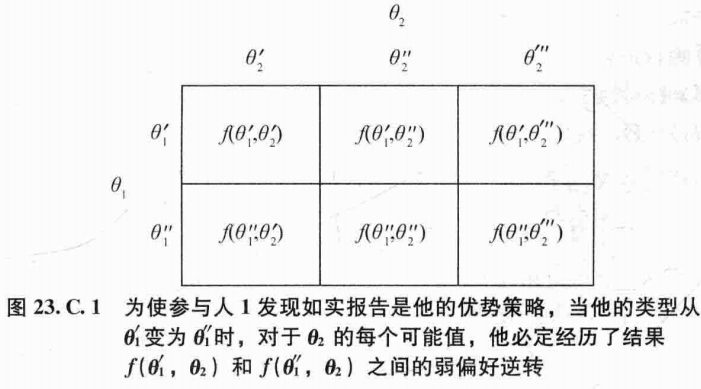
在图中，我们以两个参与人（\(I=2\)）、类型 \(\theta_1\) 有两个可能值、类型 \(\theta_2\) 有三个可能值为例，画出了对于每个可能类型组合 \((\theta_1, \theta_2)\) 的社会选择函数 \(f\)。考虑参与人 1 如实报告的激励。如果如实报告是参与人 1 的一个弱占优策略，那么当他的类型从 \(\theta_1'\) 变为 \(\theta_1''\) 时，对于 \(\theta_2\) 的每个可能值，他必定经历了结果 \(f(\theta_1', \theta_2)\) 和 \(f(\theta_1'', \theta_2)\) 之间的弱偏好逆转。类似的结论对于参与人 2 也成立。

吉巴德-萨特斯韦特定理¶

吉巴德-萨特斯韦特定理（Gibbard-Satterthwaite theorem）是由 Gibbard（1973）和 Satterthwaite（1975）在 20 世纪 70 年代独立发现的。它在性质上是个类似于阿罗不可能定理的一个不可能结论。这个定理在很大程度上塑造了关于激励与执行问题研究的进程。它表明，对于很大一类问题来说，不可能在占优策略中执行令人满意的社会选择函数。

令 \(\mathcal{P}\) 表示 \(X\) 上的所有偏好关系 \(\succeq\) 组成的集合，而且在这个集合中任何两个备选方案都不是无差异的。在微观经济学的社会选择一讲中我们说过 \(\mathcal{R}_i = \{ \succeq_i \mid \succeq_i = \succeq_i(\theta) \}\) 是参与人 \(i\) 在 \(X\) 上的可能序数偏好关系集。我们把 \(f(\cdot)\) 的像记为 \(f(\Theta)\)，也就是说，

\[ f(\Theta) = \{ x \in X \mid f(\theta) = x\ \text{对于某个}\ \theta \in \Theta \} \]

即 \(f(\Theta)\) 是 \(f\) 在 \(\Theta\) 下的所有可能选择结果。下面的定义 3 和定义 4 我们回忆社会选择一讲中讨论的社会选择函数的两个性质：

定义 3：独裁性

社会选择函数 \(f(\cdot)\) 是独裁的（dictatorial），如果存在一个参与人 \(i\) 使得对于所有 \(\theta = (\theta_1, \cdots, \theta_I) \in \Theta\)，我们有

\[ f(\theta) \in \{ x \in X \mid \succeq_i(x, \theta_i) \geqslant \succeq_i(y, \theta_i)\ \text{对于所有}\ y \in X \} \]

用文字表示：对于某个社会选择函数来说，如果存在一个参与人 \(i\) 使得 \(f(\cdot)\) 总是在 \(i\) 的排在最前面的备选方案中选择一个，那么我们说该社会选择函数是独裁的。

定义 4：单调性

社会选择函数 \(f(\cdot)\) 是单调的（monotonic），如果对于任何 \(\theta\)，如果 \(\theta'\) 满足对于所有 \(i\) 都有 \(L_i(f(\theta), \theta_i) \subset L_i(f(\theta), \theta_i')\)，那么 \(f(\theta') = f(\theta)\)。

单调性要求，假设 \(f(\theta) = x\)，而且 \(I\) 个参与人的类型变为 \(\theta' = (\theta_1', \cdots, \theta_I')\) 后，如果当参与人 \(i\) 的类型为 \(\theta_i\) 时某个对他来说弱劣于 \(x\) 的备选方案，不会在他的类型变为 \(\theta_i'\) 后严格优于 \(x\)，那么 \(x\) 必定也是 \(\theta'\) 下的社会选择。事实上这与之前定义的单调性内涵一致，即原先就选择了 \(x\)，现在有些参与人觉得 \(x\) 还更好了，那么之后社会选择仍然也是 \(x\)。

注：单调性只是社会选择函数的一个分析性质，在单调性的描述中参与人的类型可能发生变化，变化前后我们都要求参与人是诚实最优的（这是激励相容定义的要求）。

有了这些定义之后，现在我们开始阐述和证明吉巴德-萨特斯韦特定理：

吉巴德-萨特斯韦特定理

假设 \(X\) 是有限的而且至少包含三个元素；\(\mathcal{R}_i = \mathcal{P}\) 对于所有 \(i\)；\(f(\Theta) = X\)。那么：社会选择函数 \(f\) 在占优策略中可如实执行当且仅当它是独裁的。

值得一提的是，这一定理其实并不一定要求 \(X\) 是有限集合，无限集合如果能保证偏好能写出相应的效用函数，则可以使用这一定理。下面我们给出这一定理的证明：

吉巴德-萨特斯韦特定理的证明

不难验证一个独裁的 \(f\) 是如实可执行的。我们现在证明如果 \(f\) 在占优策略中如实可执行，那么它必定是独裁的。证明分成三步。

第 1 步：如果 \(\mathcal{R}_i = \mathcal{P}\) 对于所有 \(i\) 成立，而且 \(f\) 在占优策略中如实可执行，那么 \(f\) 是单调的。

考虑两个类型组合 \(\theta\) 和 \(\theta'\) 使得 \(L_i(f(\theta), \theta_i) \subset L_i(f(\theta), \theta_i')\) 对于所有 \(i\) 成立。我们希望证明 \(f(\theta) = f(\theta')\)。我们首先确定 \(f(\theta_1', \theta_2, \cdots, \theta_I)\)。由于 \(f\) 在占优策略中如实可执行，根据本讲之前提到的“占优策略激励相容的另一种刻画”，我们知道

\(f(\theta_1', \theta_2, \cdots, \theta_I) \in L_1(f(\theta), \theta_1)\) 成立，即 \(f(\theta) \succeq_{\theta_1} f(\theta_1', \theta_2, \cdots, \theta_I)\)，根据 \(L_i(f(\theta), \theta_i) \subset L_i(f(\theta), \theta_i')\) 可知，\(f(\theta) \succeq_{\theta_1'} f(\theta_1', \theta_2, \cdots, \theta_I)\)
\(f(\theta) \in L_1(f(\theta_1', \theta_2, \cdots, \theta_I), \theta_1')\) 成立，即 \(f(\theta_1', \theta_2, \cdots, \theta_I) \succeq_{\theta_1'} f(\theta)\)。

根据假设，在偏好关系 \(\succeq_1(\theta_1')\) 中任何两个备选方案都不是无差异的，这必定意味着 \(f(\theta_1', \theta_2, \cdots, \theta_I) = f(\theta)\). 使用相同的论证思路可以证明 \(f(\theta_1', \theta_2', \theta_3', \cdots, \theta_I) = f(\theta)\)。事实上，如此迭代下去，我们就能得到 \(f(\theta') = f(\theta)\)。因此，\(f\) 是单调的。

第 2 步：如果 \(\mathcal{R}_i = \mathcal{P}\) 对于所有 \(i\) 成立，而且 \(f\) 是单调的，以及 \(f(\Theta) = X\)，那么 \(f\) 为事后有效率的。

反证法。假设 \(f\) 不是事后有效率的，那么存在一个 \(\theta \in \Theta\) 和一个 \(y \in X\) 使得 \(u_i(y, \theta_i) > u_i(f(\theta), \theta_i)\) 对于所有 \(i\) 成立（记住，任何两个备选方案都不是无差异的）。因为 \(f(\Theta) = X\)，所以存在一个 \(\theta' \in \Theta\) 使得 \(f(\theta') = y\)。

由于 \(\mathcal{R}_i = \mathcal{P}\)，故我们可以选出关于类型的一个向量 \(\theta'' \in \Theta\) 使得对所有 \(i\)，对于所有 \(z \neq f(\theta), y\) 都有 \(u_i(y, \theta_i'') > u_i(f(\theta), \theta_i'') > u_i(z, \theta_i'')\) 成立。从而我们有 \(L_i(y, \theta_i') \subset L_i(y, \theta_i'')\) 对于所有 \(i\) 成立，单调性意味着 \(f(\theta'') = y\)。但是，由于 \(L_i(f(\theta), \theta_i) \subset L_i(f(\theta), \theta'')\) 对于所有 \(i\) 也成立，单调性也意味着 \(f(\theta'') = f(\theta)\)，这样我们就得到了一个矛盾，因为 \(y \neq f(\theta)\)。因此，\(f\) 必定是事后有效率的。

注：第 2 步的核心思想就是，构造一个特殊的偏好关系 \(\theta_i''\)，然后通过单调性得到在 \(\theta_i''\) 下社会选择出现矛盾。

第 3 步：若社会选择函数 \(f\) 是单调的和事后有效率的，则 \(f\) 必然是独裁的。

在微观经济学的社会选择一讲最后我们证明了“备选方案数量至少有三个，可行偏好组合的定义域为 \(\mathcal{A} = \mathcal{R}^I\) 或 \(\mathcal{A} = \mathcal{P}^I\) 时，每个弱帕累托的和单调的社会选择函数 \(f : \mathcal{A} \to X\) 是独裁的”，这是直接的推论。

需要指出，如果 \(X\) 仅含有两个元素，那么吉巴德-萨特斯韦特定理的结论不成立。例如，在这种情形下，不难验证多数投票社会选择函数在占优策略中如实可执行，但不是独裁的。另外，还需要注意当 \(\mathcal{R}_i = \mathcal{P}\) 对于所有 \(i\) 成立时，任何事后有效率的社会选择函数必定有 \(f(\Theta) = X\)（因为总可以构造出特殊的偏好让所有人都最喜欢任意的 \(x \in X\)）。因此，吉巴德-萨特斯韦特定理表明，当 \(\mathcal{R}_i = \mathcal{P}\) 对于所有 \(i\) 成立且 \(X\) 的元素多于两个时，唯一能在占优策略中如实执行的事后有效率的社会选择函数，是独裁的社会选择函数。

给定这个令人沮丧的结论，如果我们想执行合意的社会选择函数，我们要么放松执行概念上的要求——使用基于相对不那么稳健的均衡概念（比如贝叶斯纳什均衡）上的执行定义；要么考察限制性更强的环境。第一条路径我们在下一讲中介绍，第二条路径我们将在接下来马上进行讨论，我们会把偏好限制在拟线性偏好上讨论。

注：我们可以在两个方向上扩展吉巴德-萨特斯韦特定理，一是考虑可能存在无差异个人偏好的情形，考虑 \(\mathcal{P} \subset \mathcal{R}_i\)；二是 \(f(\Theta) \subsetneq X\) 的情形。此处不再赘述，感兴趣的读者可以参考 MWG《微观经济学》第 23.C 中间的小字部分。

拟线性环境：VCG 机制¶

基本形式与例子¶

在本小节，我们主要考察参与人的偏好为拟线性的情形，这是一种特殊情形但广受关注（在拍卖理论等非常常见）。特别地，现在一个备选方案为一个向量 \(x = (k, t_1, \cdots, t_I)\)，其中 \(k\) 是一个项目选择，\(t_i\) 是转移给参与人 \(i\) 的计价物商品（“钱”）。参与人 \(i\) 的效用函数为拟线性形式

\[ u_i(x, \theta_i) = v_i(k, \theta_i) + (\overline{m}_i + t_i) \]

其中 \(\overline{m}_i\) 是参与人 \(i\) 的计价物禀赋。上面的表达式的拟线性性体现在我们将 \(k\) 的决策的效用与计价物的效用分离成了拟线性形式。接下来假设我们的环境是个封闭系统，也就是说这 \(I\) 个参与人无法向外界借贷资金。因此，备选方案集为

\[ X = \{ (k, t_1, \cdots, t_I) \mid k \in K, t_i \in \mathbb{R}, \sum\limits_{i=1}^I t_i \leqslant 0 \} \]

注意到，这种环境包括例 2 和例 3 中的情形：

例 2：公共项目（续）

令 \(K\) 包含该公共项目的所有可能水平（例如，如果 \(K = \{0, 1\}\)，这是说项目有两个水平：“不实施”或“实施”），令 \(c(k)\) 表示公共项目水平 \(k \in K\) 的成本。假设 \(\tilde{v}_i(k, \theta_i)\) 是参与人 \(i\) 从项目水平 \(k\) 得到的总收益，而且如果不进行其他转移，那么项目资金将由参与人平均分摊（即，每个参与人支付 \(c(k)/I\)）。因此，当参与人 \(i\) 的类型为 \(\theta_i\) 时，我们可以将他从水平 \(k\) 得到的净收益写为 \(v_i(k, \theta_i) = \tilde{v}_i(k, \theta_i) - c(k)/I\)。现在 \(t_i\) 是超过 \(c(k)/I\) 那部分的货币转移。

注：这里做出这样的调整的目的是为了后面 \(t_i\) 求和的要求以及预算平衡的定义等在这一例子下也是适用的。

例 3：一单位某种不可分割私人物品的分配（续）

参与人有 \(I\) 个，我们打算将一单位某种不可分割私人物品分配给其中一个参与人。在这里，“项目选择” \(k = (y_1, \cdots, y_I)\) 表示私人物品的分配，\(K = \{ (y_1, \cdots, y_I) \mid y_i \in \{0, 1\}\ \text{对于所有}\ i\ \text{和}\ \sum\limits_{i=1}^I y_i = 1 \}\)。参与人的评价函数形式为 \(v_i(k, \theta_i) = \theta_i y_i\)。

在这种拟线性环境中，社会选择函数的形式为 \(f(\cdot) = (k(\cdot), t_1(\cdot), \cdots, t_I(\cdot))\)。其中对于所有 \(\theta \in \Theta\)，\(k(\theta) \in K\) 和 \(\sum\limits_{i=1}^I t_i(\theta) \leqslant 0\)。注意到，如果社会选择函数 \(f\) 是事后有效率的，那么对于所有 \(\theta \in \Theta\)，\(k(\theta)\) 必定满足

\[ \sum\limits_{i=1}^I v_i(k(\theta), \theta_i) \geqslant \sum\limits_{i=1}^I v_i(k, \theta_i), \forall k \in K \tag{4} \label{mech-dom-4} \]

否则我们一定可以通过调整 \(t_i\) 的值找到一个帕累托改进。于是在拟线性环境中，事后有效率就是所谓的社会福利最大化。下面我们引入一个命题，它识别出了一类社会选择函数，这类函数满足 \(\eqref{mech-dom-4}\) 而且在占优策略中如实可执行：

VCG 机制

令 \(k^*(\cdot)\) 是满足式 \(\eqref{mech-dom-4}\) 的一个函数。如果对于所有 \(i = 1, \cdots, I\)，我们有

\[ t_i(\theta) = \left[ \sum\limits_{j \neq i} v_j(k^*(\theta), \theta_j) \right] + h_i(\theta_{-i}) \tag{5} \label{mech-dom-5} \]

其中 \(h_i(\cdot)\) 是一个关于 \(\theta_i\) 的任意函数，那么社会选择函数 \(f(\cdot) = (k^*(\cdot), t_1(\cdot), \cdots, t_I(\cdot))\) 在占优策略中如实可执行。

VCG 机制的性质证明

如果如实报告不是某个参与人 \(i\) 的占优策略，那么存在 \(\theta_i, \theta_i'\) 和 \(\theta_{-i}\) 使得

\[ v_i(k^*(\theta_i',\theta_{-i}), \theta_i) + t_i(\theta_i', \theta_{-i}) > v_i(k^*(\theta), \theta_i) + t_i(\theta) \]

使用式 \(\eqref{mech-dom-5}\) 替换上式中的 \(t_i(\theta_i', \theta_{-i})\) 和 \(t_i(\theta_i, \theta_{-i})\)，可得

\[ \sum\limits_{i=1}^I v_i(k^*(\theta_i',\theta_{-i}), \theta_i) > \sum\limits_{i=1}^I v_i(k^*(\theta), \theta_i) \]

这与 \(k^*(\cdot)\) 满足式 \(\eqref{mech-dom-4}\) 矛盾。因此，\(f(\cdot)\) 必定在占优策略中如实可执行。

满足 \(\eqref{mech-dom-4}\) 和 \(\eqref{mech-dom-5}\) 的直接显示机制 \(\Gamma = (\Theta_1, \cdots, \Theta_I, f(\cdot))\) 称为维克里-克拉克-格罗夫斯（Vickrey-Clarke-Groves）机制，简称 VCG 机制，或称格罗夫斯方案（Groves scheme, 1973）。在 VCG 机制中，给定参与人 \(j \neq i\) 的报告 \(\theta_{-i}\)，参与人 \(i\) 的转移取决于他报告的类型，这种依赖仅通过他的报告对项目选择 \(k^*(\theta)\) 的影响而发生。而且，当他的报告改变了项目决策 \(k\) 时，参与人 \(i\) 的转移改变量正好等于 \(k\) 的这个改变对参与人 \(j \neq i\) 的影响。换句话说，参与人 \(i\) 的转移的改变正好反映了他对其他参与人施加的外部性（externality）。因此，这诱导参与人 \(i\) 将该外部性内部化，并且如实报告类型，从而产生了 \(k\) 的最优水平，即能使 \(\sum\limits_{i=1}^I v_i(k,\theta_i)\) 最大的项目水平。

Clarke（1971）独立发现了 VCG 机制的一种特殊情形，称为克拉克机制（Clarke mechanism）或主角机制（pivotal mechanism）。这个机制对应于 \(h_i(\theta_{-i}) = -\sum\limits_{j \neq i} v_j(k_{-i}^*(\theta_{-i}), \theta_j)\) 的情形，其中对于所有 \(\theta_{-i} \in \Theta_{-i}\)，\(k_{-i}^*(\theta_{-i})\) 满足

\[ \sum\limits_{j \neq i} v_j(k_{-i}^*(\theta_{-i}), \theta_j) \geqslant \sum\limits_{j \neq i} v_j(k, \theta_j), \forall k \in K \]

也就是说，如果只有 \(I-1\) 个参与人 \(j \neq i\)，\(k_{-i}^*(\theta_{-i})\) 是事后有效率的项目水平，即 \(k_{-i}^*\) 就是使得 \(I-1\) 个参与人 \(j \neq i\) 福利最大化的结果。于是，在克拉克机制中，参与人 \(i\) 的支付为

\[ t_i(\theta) = \left[ \sum\limits_{j \neq i} v_j(k^*(\theta), \theta_j) \right] - \left[ \sum\limits_{j \neq i} v_j(k_{-i}^*(\theta_{-i}), \theta_j) \right] \]

注意到，相对于参与人 \(j \neq i\) 的事后有效率项目水平来说，如果参与人 \(i\) 的报告没有改变项目决策（即，如果 \(k^*(\theta) = k_{-i}^*(\theta_{-i})\)），那么参与人 \(i\) 的转移为零；如果他的报告改变了项目决策（即，如果 \(k^*(\theta) \neq k_{-i}^*(\theta_{-i})\)），也就是说，如果参与人 \(i\) 对于有效率的项目选择来说是起决定作用的“主角”，那么他的转移为负。因此，在克拉克机制中，如果参与人 \(i\) 对于项目决策来说是主角，那么他缴纳的税收额等于他对其他参与人施加的外部性，如果他不是主角，他不需要缴税。

令人感兴趣的是，这正是所谓 VCG 拍卖的支付函数（之后的拍卖理论我们会进一步介绍），并且在一单位某种不可分割私人物品的分配问题中，克拉克机制正好是由第二价格密封拍卖（又称 Vickrey 拍卖）执行的社会选择函数。特别地：

\(k^*(\theta)\) 是一种分配规则，它将物品卖给对该物品评价最高的人；
当参与人 \(i\) 是对物品的评价最高的买者时，他正好是主角；
当参与人 \(i\) 是主角时，他缴纳的“税收”正好等于第二高的评价（特别地，在这种情形下 \(\sum\limits_{j \neq i} v_j(k^*(\theta), \theta_j) = 0\)，而且 \(\sum\limits_{j \neq i} v_j(k_{-i}^*(\theta_{-i}), \theta_j)\) 等于第二高评价数额）。

到目前为止我们已经看到，满足式 \(\eqref{mech-dom-4}\) 和 \(\eqref{mech-dom-5}\) 的社会选择函数在占优策略中如实可执行。这类函数是满足式 \(\eqref{mech-dom-4}\) 且是如实可执行的唯一函数吗？下面的命题（归功于 Green 和 Laffont，1979）表明，在一定条件下，答案是肯定的。在这个命题中，我们令 \(V\) 表示由所有可能函数 \(v : K \to \mathbb{R}\) 组成的集合。

Green 和 Laffont，1979

假设对于每个参与人 \(i = 1, \cdots, I\)，、对于某个 \(\theta_i \in \Theta_i\)，每个可能评价函数 \(v_i : K \to \mathbb{R}\) 都可能出现。那么对于某个社会选择函数 \(f(\cdot) = (k^*(\cdot), t_1(\cdot), \cdots, t_I(\cdot))\) 来说（其中 \(k^*\) 满足 \(\eqref{mech-dom-4}\)），\(f(\cdot)\) 在占优策略中如实可执行仅当对于 \(i = 1, \cdots, I\)，\(t_i(\cdot)\) 满足式 \(\eqref{mech-dom-5}\)。

证明

首先注意到我们总可以将 \(t\) 的表达式写为（因为 \(h\) 可以是任意函数）

\[ t_i(\theta_i, \theta_{-i}) = \sum\limits_{j \neq i} v_j(k^*(\theta_i,\theta_{-i}), \theta_j) + h_i(\theta_i, \theta_{-i}) \tag{6} \label{mech-dom-6} \]

于是我们想证明的是，如果 \(f(\cdot)\) 在占优策略中如实可执行，函数 \(h_i(\cdot)\) 必定事实上独立于 \(\theta_i\)。假设它不是；也就是说，\(f(\cdot)\) 在占优策略中如实可执行，但是对于某个 \(\theta_i, \theta_i'\) 和 \(\theta_{-i}\)，我们有 \(h_i(\theta_i, \theta_{-i}) \neq h_i(\theta_i', \theta_i)\)。现在我们考虑两种不同的情形。

\(k^*(\theta_i, \theta_{-i}) = k^*(\theta_i', \theta_{-i})\)：如果 \(f(\cdot)\) 在占优策略中如实可执行，那么根据式 \(\eqref{mech-dom-3}\) 我们有

\[ v_i(k^*(\theta_i, \theta_{-i}), \theta_i) + t_i(\theta_i, \theta_{-i}) \geqslant v_i(k^*(\theta_i', \theta_{-i}), \theta_i) + t_i(\theta_i', \theta_{-i}) \]

和

\[ v_i(k^*(\theta_i', \theta_{-i}), \theta_i') + t_i(\theta_i', \theta_{-i}) \geqslant v_i(k^*(\theta_i, \theta_{-i}), \theta_i') + t_i(\theta_i, \theta_{-i}) \]

由于 \(k^*(\theta_i, \theta_{-i}) = k^*(\theta_i', \theta_{-i})\)，上述两个不等式意味着 \(t_i(\theta_i, \theta_{-i}) = t_i(\theta_i', \theta_{-i})\)，因此根据式 \(\eqref{mech-dom-6}\) 我们有 \(h_i(\theta_i, \theta_{-i}) = h_i(\theta_i', \theta_{-i})\)：矛盾。
\(k^*(\theta_i, \theta_{-i}) \neq k^*(\theta_i', \theta_{-i})\)：不失一般性，假设 \(h_i(\theta_i, \theta_{-i}) > h_i(\theta_i', \theta_{-i})\)。考虑满足下列条件的类型 \(\theta^{\epsilon}_i \in \Theta_i\)：

\[ v_i(k, \theta_i^{\epsilon}) = \begin{cases} -\sum\limits_{j \neq i} v_j(k^*(\theta_i, \theta_{-i}), \theta_j) & \text{if}\ k = k^*(\theta_i, \theta_{-i}) \\ -\sum\limits_{j \neq i} v_j(k^*(\theta_i', \theta_{-i}), \theta_j) + \epsilon & \text{if}\ k = k^*(\theta_i', \theta_{-i}) \\ -\infty & \text{otherwise} \end{cases} \tag{7} \label{mech-dom-7} \]

我们将证明，对于充分小的 \(\epsilon > 0\)，当其他参与人的类型为 \(\theta_{-i}\) 时，类型为 \(\theta^{\epsilon}_i\) 的参与人严格偏好说谎，谎称自己的类型为 \(\theta_i\)。为了看清这一点，首先注意到，\(k^*(\theta_i', \theta_{-i}) = k^*(\theta_i^{\epsilon}, \theta_{-i})\)，这是因为根据 \(\eqref{mech-dom-7}\) 可知 \(k = k^*(\theta_i', \theta_{-i})\) 使得社会福利 \(v_i(k, \theta^{\epsilon}_i) + \sum\limits_{j \neq i} v_j(k, \theta_j)\) 最大。因此，为使如实报告成为占优策略，必有

\[ v_i(k^*(\theta_i', \theta_{-i}), \theta^{\epsilon}_i) + t_i(\theta^{\epsilon}_i, \theta_{-i}) \geqslant v_i(k^*(\theta_i, \theta_{-i}), \theta^{\epsilon}_i) + t_i(\theta_i, \theta_{-i}) \]

或者根据式 \(\eqref{mech-dom-6}\) 和式 \(\eqref{mech-dom-7}\) 进行代换可得

\[\epsilon + h_i(\theta_i^{\epsilon}, \theta_{-i}) \geqslant h_i(\theta_i, \theta_{-i})\]

然后同证明的第 1 部分的逻辑可知，\(h_i(\theta^{\epsilon}_i, \theta_{-i}) = h_i(\theta_i', \theta_{-i})\)，这是因为 \(k^*(\theta^{\epsilon}_i, \theta_{-i}) = k^*(\theta_i', \theta_{-i})\)。由此可得

\[\epsilon + h_i(\theta_i', \theta_{-i}) \geqslant h_i(\theta_i, \theta_{-i}) \]

根据假设我们有 \(h_i(\theta_i, \theta_{-i}) > h_i(\theta_i', \theta_{-i})\)，因此，对于足够小的 \(\epsilon > 0\)，上式必定不成立。这样我们就完成了证明。

因此，对于某个 \(\theta_i \in \Theta_i\)，每个可能评价函数 \(v_i(k, \theta_i)\) 都可能出现的情形下，满足 \(\eqref{mech-dom-4}\) 且在占优策略中如实可执行的唯一一类社会选择函数是 VCG 机制中的社会选择函数。

VCG 机制与预算平衡¶

直到目前，我们已经研究了对于总是能导致 \(k\) 的有效率选择的社会选择函数（满足 \(\eqref{mech-dom-4}\) 的函数）何时能在占优策略中如实执行。但是事后效率也要求计价物不存在浪费，也就是说，要求满足预算平衡条件：

\[ \sum\limits_{i=1}^I t_i(\theta) = 0, \forall \theta \in \Theta \tag{8} \label{mech-dom-8} \]

我们现在简要考察完全事后有效率的社会选择函数（满足 \(\eqref{mech-dom-4}\) 和 \(\eqref{mech-dom-8}\) 的函数）何时能在占优策略中如实执行。遗憾的是，在很多情形下我们不可能在占优策略中如实执行完全事后有效率的社会选择函数。例如，下面的命题（归功于 Green 和 Laffont，1979）表明，如果每个参与人的可能类型集都充分大，那么任何在占优策略中如实可执行的社会选择函数都不是事后有效率的。这个命题的证明我们略去。

Green 和 Laffont，1979

假设对于每个参与人 \(i = 1, \cdots, I\)，每个可能评价函数 \(v_i: K \to \mathbb{R}\) 都可能出现。那么不存在社会选择函数 \(f(\cdot) = (k^*(\cdot), t_1(\cdot), \cdots, t_I(\cdot))\) 满足 \(\eqref{mech-dom-4}\) 和 \(\eqref{mech-dom-8}\)（即满足事后有效率），且在占优策略中如实可执行。

因此，在上述命题的假设下，私人信息的存在意味着 \(I\) 个参与人要么容忍计价物的浪费（即对于某个 \(\theta\) 有 \(\sum\limits_{i=1}^I t_i(\theta) < 0\)，这与克拉克机制情形一样），要么不再指望总能得到有效率的项目选择（即对于某个 \(\theta\)，未必满足 \(\eqref{mech-dom-4}\)）。

当然，在一种特殊情形下，我们也能得到更为肯定的结果，这就是当至少一个参与人的偏好信息为大家共知时。为了方便表达，令这个参与人为“参与人 0”；另外，令还有 \(I\) 个参与人 \(i = 1, \cdots, I\)，这 \(I\) 个人的偏好都是私人信息（因此，现在一共有 \(I+1\) 个参与人）。最简单情形当然是，参与人 0 对项目选择 \(k\) 没有偏好，也就是说，他的偏好为 \(u_i(x) = \overline{m}_0 + t_0\)（事实上拍卖环境符合这一假定，参与人 0 就是卖家）。在这个 \(I+1\) 个参与人环境中，VCG 机制是事后有效率的，只要我们令参与人 0 的转移为 \(t_0(\theta) = -\sum\limits_{i=1}^I t_i(\theta)\) 对于所有 \(\theta\)。在本质上，无私人信息的“外部”参与人 0 的存在，使得那些拥有私人信息的参与人不需要满足预算平衡条件（VCG 拍卖就是如此）。然而，我们应该对这个貌似正面的结果提出警告：直到目前，我们还未考虑过参与人是否愿意参与到机制中。正如我们将在下一讲中看到的，当参与人自愿参与时，即使存在这样的参与人 0，也可能不存在占优策略中可执行的事后有效率社会选择函数。

可微情形¶

我们经常会遇到下列情形：\(K = \mathbb{R}\)，\(v_i(k, \theta_i)\) 是二次连续可微的，而且在所有 \((k, \theta_i)\) 上，

\[ \dfrac{\partial^2 v_i(k, \theta_i)}{\partial k^2} < 0, \dfrac{\partial^2 v_i(k, \theta_i)}{\partial k \partial \theta_i} \neq 0 \]

并且每个 \(\theta_i\) 是从区间 \([\underline{\theta}_i, \overline{\theta}_i] \subset \mathbb{R}\) 中抽取出的（其中 \(\underline{\theta}_i \neq \overline{\theta}_i\)）。在这种情形下，关于社会选择函数集有很多值得探讨的地方，此处我们主要证明，在这个环境中如何轻松地得到前文的一些结果。

首先注意到，对于任何连续可微的社会选择函数 \(f(\cdot) = (k(\cdot), t_1(\cdot), \cdots, t_I(\cdot))\)，如果如实报告是参与人 \(i\) 的一个占优策略，那么参与人 \(i\) 的一阶条件意味着，对于所有 \(\theta_i\)，在所有 \(\theta_i \in (\theta, \theta')\) 上，我们有

\[ \dfrac{\partial v_i(k(\theta_i, \theta_{-i}), \theta_i)}{\partial k} \dfrac{\partial k(\theta_i, \theta_{-i})}{\partial \theta_i} + \dfrac{\partial t_i(\theta_i, \theta_{-i})}{\partial \theta_i} = 0 \tag{9} \label{mech-dom-9} \]

将上式关于变量 \(\theta_i\) 积分，这意味着对于所有类型组合 \((\theta, \theta_{-i})\)，我们有

\[ t_i(\theta_i, \theta_{-i}) = t_i(\underline{\theta}_i, \theta_{-i}) - \int_{\underline{\theta}_i}^{\theta} \dfrac{\partial v_i(k(s, \theta_{-i}), s)}{\partial k} \dfrac{\partial k(s, \theta_{-i})}{\partial s} \text{d}s \tag{9} \label{mech-dom-10} \]

现在考虑满足式 \(\eqref{mech-dom-4}\) 的任何社会选择函数 \(f(\cdot) = (k^*(\cdot), t_1(\cdot), \cdots, t_I(\cdot))\)。在我们当前的假设条件下，\(k^*(\cdot)\) 必定满足：对于所有 \(\theta\)，

\[ \sum\limits_{i=1}^I \dfrac{\partial v_i(k^*(\theta), \theta_i)}{\partial k} = 0 \tag{10} \label{mech-dom-11} \]

而且，使用隐函数定理和我们对函数 \(v_i(\cdot)\) 所作的假设，可知 \(k^*(\cdot)\) 是连续可微的，而且它有着非零偏导数 \(\dfrac{\partial k^*(\theta)}{\partial \theta_i} \neq 0\) 对于所有 \(i\)。现在我们使用式 \(\eqref{mech-dom-11}\) 替换式 \(\eqref{mech-dom-10}\) 中的 \(\dfrac{\partial v_i(k(s, \theta_{-i}), s)}{\partial k}\)。替换后可知，对于所有组合 \((\theta, \theta_{-i})\)，

\[ \begin{aligned} t_i(\theta, \theta_{-i}) & = t_i(\underline{\theta}_i, \theta_{-i}) + \int_{\underline{\theta}_i}^{\theta} \left(\sum\limits_{j \neq i} \dfrac{\partial v_j(k^*(s, \theta_{-i}), \theta_j)}{\partial k}\right) \dfrac{\partial k^*(s, \theta_{-i})}{\partial s} \text{d}s \\ & = t_i(\underline{\theta}_i, \theta_{-i}) + \int_{k^*(\underline{\theta}_i, \theta_{-i})}^{k^*(\theta, \theta_{-i})} \left(\sum\limits_{j \neq i} \dfrac{\partial v_j(k, \theta_j)}{\partial k}\right) \text{d}k \\ &= t_i(\underline{\theta}_i, \theta_{-i}) + \sum\limits_{j \neq i} v_j(k^*(\theta, \theta_{-i}), \theta_j) - \sum\limits_{j \neq i} v_j(k^*(\underline{\theta}_i, \theta_{-i}), \theta_j) \end{aligned} \]

但这为真当且仅当 \(t_i(\theta)\) 满足 \(\eqref{mech-dom-5}\)。因此，在这样的环境下，格罗夫斯机制是在占优策略中如实可执行且满足 \(\eqref{mech-dom-4}\) 的唯一一类社会选择函数。

现在考虑当不存在外部参与人 0 时的预算平衡问题。我们将证明，当 \(I=2\) 时（对于 \(I > 2\) 参见 Laffont 和 Maskin（1980）），在这个可微环境中，不可能满足 \(\eqref{mech-dom-11}\) 和预算平衡条件。根据 \(\eqref{mech-dom-9}\) 可知，对于所有 \(\theta=(\theta_1, \theta_2)\)，我们有

\[ \dfrac{\partial t_1(\theta)}{\partial \theta_1} = - \dfrac{\partial v_1(k^*(\theta), \theta_1)}{\partial k} \dfrac{\partial k^*(\theta)}{\partial \theta_1} \]

和

\[ \dfrac{\partial t_2(\theta)}{\partial \theta_2} = - \dfrac{\partial v_2(k^*(\theta), \theta_2)}{\partial k} \dfrac{\partial k^*(\theta)}{\partial \theta_2} \]

因此，对于所有 \(\theta=(\theta_1, \theta_2)\)，

\[ - \dfrac{\partial^2 t_1(\theta)}{\partial \theta_1\partial \theta_2} = \dfrac{\partial^2 v_1(k^*(\theta), \theta_1)}{\partial k^2} \dfrac{\partial k^*(\theta)}{\partial \theta_2} \dfrac{\partial k^*(\theta)}{\partial \theta_1} + \dfrac{\partial v_1(k^*(\theta), \theta_1)}{\partial k} \dfrac{\partial^2 k^*(\theta)}{\partial \theta_1\partial \theta_2} \]

和

\[ - \dfrac{\partial^2 t_2(\theta)}{\partial \theta_1\partial \theta_2} = \dfrac{\partial^2 v_2(k^*(\theta), \theta_2)}{\partial k^2} \dfrac{\partial k^*(\theta)}{\partial \theta_2} \dfrac{\partial k^*(\theta)}{\partial \theta_1} + \dfrac{\partial v_2(k^*(\theta), \theta_2)}{\partial k} \dfrac{\partial^2 k^*(\theta)}{\partial \theta_1\partial \theta_2} \]

如果预算平衡，那么 \(t_1(\theta) = -t_2(\theta)\) 对于所有 \(\theta\) 成立，因此我们必定有 \(\dfrac{\partial^2 t_1(\theta)}{\partial \theta_1\partial \theta_2} = -\dfrac{\partial^2 t_2(\theta)}{\partial \theta_1\partial \theta_2}\)。但这意味着，通过将上述两个式子相加，并使用 \(\eqref{mech-dom-10}\)，即可得到

\[ \left[ \dfrac{\partial^2 v_1(k^*(\theta), \theta_1)}{\partial k^2} + \dfrac{\partial^2 v_2(k^*(\theta), \theta_2)}{\partial k^2} \right] \dfrac{\partial k^*(\theta)}{\partial \theta_1} \dfrac{\partial k^*(\theta)}{\partial \theta_2} = 0 \]

但在我们的假设条件下，这是不可能的。