最优机制¶
本讲我们将探讨最优机制的问题:考虑一个卖家有一个不可分割的物品要出售的场景,卖家对潜在买家的支付意愿具有不完全信息,问如何设计一个机制使得卖家能够获得最大的期望收益。这一问题在 Myerson 在 1981 年的一篇经典论文 Optimal Auction Design 中解决,本讲内容就是遵循着论文的逻辑展开的。
问题描述¶
我们考虑一个卖家有一个不可分割的物品要出售的场景,有 \(n\) 个潜在的买家 \(N = \{1, 2, \ldots, n\}\)。每个买家 \(i\) 对物品的心理价位对卖家以及其它买家而言是不完全信息,我们用连续型随机变量 \(t_i\) 描述(这一随机变量是共同知识),其概率密度函数 \(f_i: [a_i,b_i] \to \mathbb{R}^+\),其中 \(a_i\) 和 \(b_i\) 是买家 \(i\) 的心理价位的上下界。我们假设 \(f_i\) 是连续的,且 \(f_i(t_i) > 0\) 对所有 \(t_i \in [a_i,b_i]\) 成立。基于上面的描述,我们有 \(t_i\) 的分布函数
分布函数在 \(t_i\) 处的值表示参与人 \(i\) 心理价位小于等于 \(t_i\) 的概率。接下来我们记 \(T\) 为所有参与人可能的估值组合,即
根据博弈论的通常记号,\(T_{-i} = [a_1,b_1] \times \cdots \times [a_{i-1},b_{i-1}] \times [a_{i+1},b_{i+1}] \times \cdots \times [a_n,b_n]\) 表示除了 \(i\) 之外的所有人的估值组合。在开始的讨论中,我们都会假定不同参与人的估值分布是相互独立的,因此在 \(T\) 上的联合密度函数是 \(f(t) = \prod\limits_{i=1}^n f_i(t_i)\),同样,按照惯例我们记 \(f_{-i}(t_{-i}) = \prod\limits_{j\in N, j \neq i} f_j(t_j)\)。
卖家对物品也有一个估值,代表这个物品没被卖出去,仍被卖家持有时卖家的效用,我们记为 \(t_0\),并假设这一信息是公开的,即所有参与人都知道卖家的估值。
在迈尔森的原文中还做了如下讨论:为什么买家(或称投标者,bidder)的估值是不完全信息的?有两点原因,其一是偏好不确定性(preference uncertainty),其二是质量不确定性(quality uncertainty)。如果只有前者,那么不同买家的估值是互不影响的,但如果是第二点,那么其他买家的估值可能会影响其他买家的估值,比如一处石油矿藏的估值,就会受到其他买家的估值的影响(因为有的买家可能具有更多的对这处矿藏质量的信息)。在这里我们只简单提及,不会在模型中出现第二点引入的参数,因为影响不大(原论文是有的,感兴趣的读者可以直接阅读原论文)。
什么是合理的机制¶
给定每个参与人的密度函数 \(f_i\),卖家的任务是设计一个机制,使得自己能够获得最大的期望收益。那么什么是合理的机制呢?事实上在机制设计的前几讲中我们已经讨论了这个问题,即我们应当考虑满足个人理性的直接显示机制(贝叶斯纳什均衡下的),在这一机制中,我们要求买家诚实报出其估价,然后卖家根据估价组合 \(t = (t_1,\cdots,t_n)\) 做出决策。显示原理告诉我们,考虑直接显示机制是不失一般性的,因为对于任何机制,我们都可以通过一个直接显示机制来模拟。在我们的场景中,直接显示机制可以用一对结果函数 \((p,x)\) 描述,其中 \(p: T \to \mathbb{R^n}\),\(p_i(t)\) 表示当所有人报价为 \(t\) 时,买家 \(i\) 得到物品的概率,称之为分配规则,\(x: T \to \mathbb{R^n}\),\(x_i(t)\) 表示当所有人报价为 \(t\) 时,买家 \(i\) 需要支付的价格,称之为支付规则。在如上的记号下,在事中阶段(即参与人知道自己的估值,对他人估值是不完全信息的阶段),参与人 \(i\) 在机制 \((p,x)\) 下的期望效用是
这应当是不难理解的,因为当所有买家报价组合为 \(t\) 时,买家的效用为他的估值乘以获得物品的概率,减去必要的支付,然后买家对其他人的报价只有一个分布,所以我们对其他人的估值取积分求期望就是买家的期望效用。类似的,卖家的期望收益是
于是我们称一个机制是合理(feasible)的当且仅当:
-
正则条件:因为只有一个物品在分配,因此对于所有 \(t \in T\),有 \(\sum\limits_{i=1}^n p_j(t) \leqslant 1\),并且 \(p_i(t) \geqslant 0\) 对所有 \(i \in N\) 和 \(t \in T\) 成立;
-
个人理性:对所有 \(i \in N\) 和 \(t_i \in [a_i,b_i]\),有 \(U_i(p,x,t_i) \geqslant 0\);
-
贝叶斯激励相容:即诚实报价是贝叶斯纳什均衡,即对所有 \(i \in N\) 和 \(t_i \in [a_i,b_i]\),有
\[ U_i(p,x,t_i) \geqslant \int_{T_{-i}} (t_ip_i(t_i',t_{-i}) - x_i(t_i',t_{-i}))f_{-i}(t_{-i}) \mathrm{d}t_{-i} \]对所有 \(t_i' \in [a_i,b_i]\) 成立。
问题的分析¶
给定机制 \((p,x)\),我们定义
则 \(Q_i(p,t_i)\) 的含义为,当参与人 \(i\) 知道自己的估值为 \(t_i\) 时,他得到物品的概率的期望。下面这一引理给出了一个机制是合理的充要条件刻画:
迈尔森引理
一个机制 \((p,x)\) 是合理的当且仅当下列条件满足:
- 若 \(s_i \leqslant t_i\),则 \(Q_i(p,s_i) \leqslant Q_i(p,t_i),\ \forall i \in N,\ \forall s_i,t_i \in [a_i,b_i]\);
- \(U_i(p,x,t_i) = U_i(p,x,a_i) + \displaystyle{\int_{a_i}^{t_i}} Q_i(p,s_i) \mathrm{d}s_i,\ \forall i \in N,\ \forall t_i \in [a_i,b_i]\);
- \(U_i(p,x,a_i) \geqslant 0,\ \forall i \in N\);
- \(\sum\limits_{i=1}^n p_j(t) \leqslant 1,\ \forall t \in T\),并且 \(p_i(t) \geqslant 0,\ \forall i \in N,\ \forall t \in T\)。
事实上第一条的含义可以更通俗地解释为:当买家 \(i\) 的估值增加时,他得到物品的概率不会减少;或者说报价的升高不会导致他得到物品的概率降低。这是很符合直观的,因为如果升高报价得到物品概率降低,显然参与人有选择不诚实地报低价的动机,当然更进一步地我们需要结合第二条给出严格证明。
迈尔森引理的证明
第 3、4 两点直接对应个人理性和正则条件,因此无需多作解释,我们只需要证明第 1、2 两点与贝叶斯激励相容性等价即可。注意到
因此贝叶斯激励相容性等价于
利用这一等价条件,我们继续迈尔森引理的证明:
-
充分性:只需证明第 1、2 两条结合起来满足 \(\eqref{myerson}\) 即可。由第二条可知,
\[ U_i(p,x,t_i) - U_i(p,x,t_i') = \int_{t_i'}^{t_i} Q_i(p,s_i) \mathrm{d}s_i \geqslant (t_i - t_i')Q_i(p,t_i') \]不等号成立是因为 \(Q_i(p,s_i)\) 是单调递增的,因此充分性得证。
-
必要性:根据 \(\eqref{myerson}\),满足贝叶斯激励相容性的机制必然有
\[\begin{gather*} U_i(p,x,t_i) - U_i(p,x,t_i') \geqslant (t_i - t_i')Q_i(p,t_i'), \\ U_i(p,x,t_i') - U_i(p,x,t_i) \geqslant (t_i' - t_i)Q_i(p,t_i), \end{gather*}\]结合上述两式,我们可以得到
\[ (t_i - t_i')Q_i(p,t_i') \leqslant U_i(p,x,t_i) - U_i(p,x,t_i') \leqslant (t_i - t_i')Q_i(p,t_i) \]不难得到第一条单调递增性成立(考虑 \(t_i > t_i'\) 和 \(t_i < t_i'\) 两种情况即可)。进一步地,三个式子均除以 \(t_i - t_i'\),然后令 \(t_i' \to t_i\),我们可以得到
\[ Q_i(p,t_i) = \dfrac{\mathrm{d}}{\mathrm{d}t_i}U_i(p,x,t_i) \]两边积分即可得到第二条,因此必要性得证。
事实上引理的第二条如果我们将 \(U_i\) 和 \(Q_i\) 的表达式展开,我们可以得到
事实上,在很多教材上,\(a_i = 0\),并且会默认 \(U_i(p,x,0) = 0\),这样的话,我们可以得到迈尔森引理的第二条的简化表达,我们可以直接利用这一公式从分配规则 \(p\) 计算得到诚实报价需要的支付规则 \(x\)(因此又被称为迈尔森支付公式),即
下图是迈尔森支付公式的一个直观解释,横坐标就是 \(t\) 的取值,\(t_i\) 在图上是 \(b_i\),很容易看出来,图上的阴影部分就是 \(x_i(t)\):
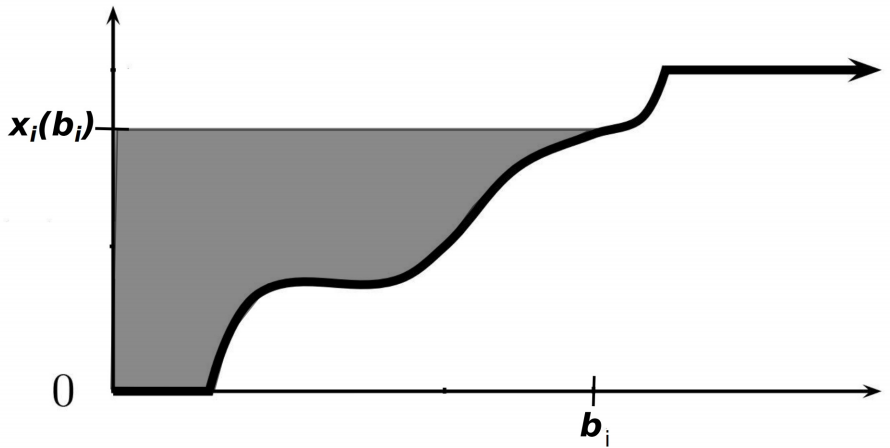
迈尔森引理给了我们刻画合理机制的一个很好的工具,接下来我们就要考察合理机制下最优机制如何导出。下面这一引理给出了最优机制的一个简洁的明了的条件:
最优机制条件
假设 \(p: T \to \mathbb{R}^n\) 最大化
且满足正则条件以及迈尔森引理的第一条。假设
那么 \((p,x)\) 是一个最优机制。
事实上这里的假设与我们上面的讨论相关,根据上面的推导,这一表达式表明最优机制下我们需要 \(U_i(p,x,a_i) = 0\),具体的原因在下面的推导中会逐渐看到:
最优机制条件的证明
回忆之前 \(U_0(p,x)\) 的表达式,我们可以将其改写为
根据 \(U_i(p,x,t_i) = t_ip_i(t) - x_i(t)\),迈尔森引理,以及 \(Q_i\) 的定义,我们有
其中第三个等号来源于累次积分交换积分次序。将这一结果代入 \(U_0(p,x)\) 的表达式,我们有
因此我们的目标是在满足迈尔森引理的四个条件的情况下最大化 \(\eqref{myerson3}\)。\(U_0\) 有两个参数,其中 \(x\) 仅出现在最后一项,因此比较容易处理,关于 \(p\) 的选择我们在之后的小节中再讨论。事实上 \(x\) 与迈尔森引理也仅仅只在第 2、3 两条中相关,显然,因为我们要求 \(U_i(p,x,a_i) \geqslant 0\),因此要最大化 \(U_0\),我们需要对于任意的 \(i\) 都有 \(U_i(p,x,a_i) = 0\),这一条件的满足只需 \(x\) 与 \(p\) 之间满足 \(\eqref{myerson2}\),是可以做到的。
除此之外,我们知道 \(\displaystyle{\int_T} t_0f(t)\) 是一个定值,因此我们的目标是最大化
故我们得到了最优机制的两个条件。
事实上,\(\eqref{myerson3}\) 的意义不仅于此,我们可以基于这一表达式得到下面这一在拍卖理论中非常重要的结论:
收入等价定理(The Revenue-Equivalence Theorem)
卖家在一个合理的拍卖机制(符合迈尔森引理要求)下的收入完全由分配机制 \(p\) 和 \(U_i(p,x,a_i)\) 决定。
这一定理的作用我们在拍卖理论中会有更多的讨论,这里我们不再展开。简单来说,一价拍卖、二价拍卖、全支付拍卖等仅在支付规则上有所不同的拍卖机制(使用显示原理转换为等价的合理机制),对于卖家而言收入是相同的。
正则化条件下的最优机制¶
下面的任务是决定最优的分配机制 \(p\) 使得 \(\eqref{myerson4}\) 最大化。事实上我们不难看出如何做到这一点——我们的方法非常直接暴力,因为最大化 \(\eqref{myerson4}\) 本质上是最大化 \(\sum\limits_{i=1}^n \left(t_i - t_0 - \dfrac{1-F_i(t_i)}{f_i(t_i)}\right)p_i(t)\),因为我们要求
实际上我们要最大化的就是 \(t_i - t_0 - \dfrac{1-F_i(t_i)}{f_i(t_i)}\) 的一个加权平均,并且我们这里需要确认的实际上就是权重。那么显然的,我们只需要给 \(t_i - t_0 - \dfrac{1-F_i(t_i)}{f_i(t_i)}\) 最大的一项或多项赋予和为 \(1\) 的权重即可,并且这一最大值必须要大于等于 \(0\),否则不如全部权重都为 \(0\) 的情况。即我们只允许同时满足
- 最大化 \(c_i(t_i) = t_i - \dfrac{1-F_i(t_i)}{f_i(t_i)}\)
- \(c_i(t_i) \geqslant t_0\)
两个条件的参与人 \(i\) 有获得物品的概率(如果有这样的参与人,他们获得物品的概率和为 \(1\))。换一种说法,即
然而我们时刻要记住,我们设计的机制必须是合理的,即满足迈尔森引理的四个条件。与 \(p\) 相关的是引理的 1、4 两条,显然第四条是满足的,因此我们只需要保证满足第一条即可。即
关于 \(s_i\) 是单调递增的。我们引入一个充分条件(正则化条件)来保证这一要求的成立:我们称这一问题符合正则化条件,如果对于任意的 \(i \in N\),都有 \(c_i(t_i)\) 关于 \(t_i\) 是严格单调递增的。这显然是 \(Q_i\) 关于 \(s_i\) 单调递增的充分条件,因为如果 \(c_i(t_i)\) 关于 \(t_i\) 严格单调递增,那么根据我们 \(p_i\) 的定义,显然当参与人 \(i\) 提高报价时,他得到物品的概率不会降低,从而 \(Q_i\) 关于 \(s_i\) 单调递增也成立。因此当满足正则化条件时,上面的机制的确是合理的最优机制。
事实上对于大部分我们熟悉的分布,正则化条件都是满足的。当然从理论层面上讲,我们仍然需要考虑正则化条件不满足的情况。当正则化条件不满足时,迈尔森引理的第一个条件也不一定满足,这样的一般情况我们在下一节中讨论。现在我们有了正则化条件下的最优机制的分配规则 \(p\),接下来我们要确定支付规则 \(x\)。如果我们令
即 \(z_i(t_{-i})\) 是使得参与人 \(i\) 刚好能有机会获得物品的最低报价,那么根据 \(\eqref{myersonpay}\),我们有
或者更简单的,如果只有一个满足 \(c_i(z_i(t_{-i})) \geqslant t_0\ \text{且}\ c_i(z_i(t_{-i})) \geqslant c_j(t_j),\ \forall j \neq i\) 的 \(i\),那么 \(p_i(t) = 1\),则有
最优机制的例子
我们考虑一种最简单的情况来具象化前面给出的结论。考虑一个所有买家估值独立同分布的情形(即对称模型),并且符合正则化条件,于是我们不难得到
结合前面得到的 \((p,x)\),我们发现此时的最优机制其实就是一个含保留价格的二价拍卖机制,其中保留价格为 \(c_i^{-1}(t_0)\)。
尽管最优机制可以使得买家获得最大的期望效用,但是这一机制存在一些天然的缺陷:
- 卖家很难准确估计每一个买家的估值分布,因此这一机制很难完美实现,之后我们也会在其他章节讨论最优机制的近似实现
- 非对称模型(即买家的估值不同分布)下,可能报价最高的买家并不是最有可能获得物品的买家。这一点非常显然,因为不同的分布下 \(c\) 的形态会有所不同。举个简单的例子,若 \(f_i(t_i) = 1/(b_i - a_i)\),即买家的估值是均匀分布,不难计算得到 \(c_i(t_i) = 2t_i - b_i\),这关于 \(t_i\) 是单调递增的,因此的确是符合正则化条件的。但是此时的最优机制是选出 \(2t_i - b_i\) 最大的 \(i\),如果 \(b_i < b_j\),那么可能存在 \(t_i < t_j\) 但是 \(2t_i - b_i > 2t_j - b_j\) 的情况,即报价更低的买家可能获得物品。
- 最优机制不是事后有效率的,例如我们考虑对称模型下,卖家 \(t_0 = 0\) 且买家估值都大于 \(0\) 的情况,此时显然物品要售出才是事后有效率(帕累托最优)的,但是如果所有买家的报价都低于 \(c_i^{-1}(0)\),那么物品就不会被售出,这显然不是事后有效率的。
一般情况下的最优机制¶
下面我们考虑正则化条件不一定满足的一般情况。注意到我们要求 \(f_i(t_i)\) 是连续的,并且在 \([a_i,b_i]\) 上取正值,因此分布函数 \(F_i(t_i)\) 是连续的且严格单调递增的,因此我们可以取到其反函数 \(F_i^{-1}: [0,1] \to [a_i,b_i]\),也是连续的且严格单调递增的。
对于每个参与人 \(i\),我们定义如下函数以便接下来的讨论。首先,对于任意的 \(q \in [0,1]\),我们定义
然后我们令 \(G_i: [0,1] \to \mathbb{R}\) 是 \(H_i\) 的凸包,即
其几何意义为,\(G_i\) 的上境图是 \(H_i\) 上境图的凸包,或者说 \(G_i\) 是 \([0,1]\) 上最大的满足 \(G_i(q) \leqslant H_i(q)\) 的凸函数。作为一个凸函数,\(G_i\) 在除可数个点之外的地方是连续可导的,并且其导数是单调递增的。我们定义 \(g_i: [0,1]\to \mathbb{R}\) 为
即 \(g_i\) 是 \(G_i\) 的导数。当然如果有不可导的点,我们可以取其右导数。进一步地,我们定义 \(\overline{c}_i: [a_i,b_i] \to \mathbb{R}\) 为
不难验证,在正则化条件满足的情况下(即 \(c_i\) 单调递增),\(G_i = H_i,\ g_i = h_i\),因此 \(\overline{c}_i = c_i\)。因此 \(\overline{c}_i\) 可以视为 \(c_i\) 在非正则情况下的一个推广。事实上整个构造函数的过程的核心也就是通过凸包强行将不一定单调递增的 \(c_i\) 推广到了一个一定单调递增的函数 \(\overline{c}_i\)(因为 \(g_i\) 和 \(G_i\) 都是单调递增的)。最后,我们定义当所有买家报价组合为 \(t\) 时,\(\overline{c}_i(t_i)\) 最大且超过 \(t_0\) 的买家的集合为
定义了如上函数后,我们可以叙述我们的核心结果:在最优机制下,物品应该分配给 \(M(t)\) 中的买家(因此正则化条件下的结果是这一结果的特例):
一般情况下的最优机制
令 \(\overline{p}: T \to \mathbb{R}^n\) 和 \(\overline{x}: T \to \mathbb{R}^n\) 满足
以及 \(\overline{x}_i(t) = t_i\overline{p}_i(t) - \displaystyle{\int_{a_i}^{t_i}} \overline{p}_i(s_i,t_{-i}) \mathrm{d}s_i\) 对任意的 \(i \in N\) 和 \(t \in T\) 成立,那么 \((\overline{p},\overline{x})\) 是一个最优机制。
一般情况下的最优机制证明
首先,使用分部积分,我们可以得到如下等式
由于 \(G_i\) 是 \(H_i\) 在 \([0,1]\) 上的凸包,因此 \(G_i(0) = H_i(0)\),\(G_i(1) = H_i(1)\),因此上式第一项为 \(0\)。接下来我们回忆最大化目标 \(\eqref{myerson4}\),我们有
注意我们 \(\overline{p}\) 选择的是最大化 \(\overline{c}_i(t_i) - t_0\) 且保证其非负的 \(i\),所以 \(\overline{p}\) 保证了上式最后一行第一项的最大化。当然 \(\overline{p}\) 也应当满足迈尔森引理的第一条(第四条显然满足),事实上也的确满足。因为 \(g_i\) 和 \(F_i\) 都是单调递增的,因此 \(\overline{c}_i\) 关于 \(t_i\) 是单调递增的,因此根据 \(M(t)\) 的定义不难看出 \(\overline{p}(t)\) 关于 \(t_i\) 是单调递增的,因此 \(Q_i(\overline{p},s_i)\) 关于 \(s_i\) 是单调递增的,因此 \(\overline{p}\) 满足迈尔森引理的第一条。
接下来我们进一步看上式最后一行的第二项。由于 \(G_i\) 是 \(H_i\) 的凸包,因此 \(H_i(F_i(t_i)) - G_i(F_i(t_i)) \geqslant 0\),并且 \(p\) 应当满足迈尔森引理第一条(即 \(Q_i\) 关于 \(s_i\) 单调递增),因此
但事实上如果我们仔细考察就会发现,因为 \(G_i\) 是 \(H_i\) 的凸包,根据几何意义不难发现(严谨证明略)当 \(G < H\) 时 \(G\) 的图像必定是平坦的(线段),即如果 \(G_i(r) < H_i(r)\),则有 \(G_i''(r) = g_i'(r) = 0\)。因此当 \(G_i(F_i(t_i)) < H_i(F_i(t_i))\) 时,\(\overline{c}_i(t_i) = g_i(F_i(t_i))\) 导数为 \(0\),因此 \(\overline{c}_i\) 在一个邻域内为常数,因此 \(\overline{p}_i\) 在一个邻域内为常数,因此 \(Q_i(\overline{p},s_i)\) 在一个邻域内为常数,因此上式最后一行第二项为 \(0\)。
因此我们的 \(\overline{p}\) 是最大化 \(\eqref{myerson4}\) 的分配规则,而 \(\overline{x}\) 之前已经验证过符合迈尔森引理的第 2、3 条,因此 \((\overline{p},\overline{x})\) 是一个最优机制。
买家估值相关的情况¶
在这一小节中,我们考虑买家估值之间的相关性。在相关的条件下,我们的一些结果可能会显得有些怪异。
买家估值相关的例子
下面的讨论将基于这一例子。为简化讨论,考虑估值分布离散的情况,假设有两个买家,每个买家对物品的估值只有两种可能:\(10\) 或 \(100\),卖家对物品的估值 \(t_0 = 0\)。假设两个买家估值的联合分布为
显然两个买家的估值不是独立的。
对于上述假设,我们考虑如下的机制:如果两个买家的出价均为 \(100\),那么随机选一个买家获得物品并支付 \(100\) 元;如果一个买家的出价为 \(100\),另一个买家的出价为 \(10\),那么出价为 \(100\) 的买家获得物品并支付 \(100\) 元,出价为 \(10\) 元的买家支付 \(30\) 元;如果两个买家的出价均为 \(10\),那么随机选一个买家获得物品并给这个买家 \(5\) 元,并给另一个买家 \(15\) 元。
总结一下,这一机制 \((p,x)\) 实际上就是:
我相信各位都会觉得这一机制非常诡异:因为甚至出现了卖家给买家钱的情况,但这事实上就是这一情况下的最优机制。不难验证诚实报价是这一机制的一个纳什均衡,并且每个买家无论其心理价位如何,在这一机制下的期望效用为 \(0\),因此买家的所有效用都被攫取了,因此这一机制是最优的。
我们来理解一下这一“诡异”的机制为什么行得通。首先,物品是分配给报价更高的买家的,这是符合单调性要求的。其次,这一机制引入了一个旁注(side bet):如果一个买家的估值为 \(10\),那么如果对方估值为 \(100\) 时自己将支付 \(30\),如果对方估值为 \(10\) 时自己得到的钱和物品的价值之和为 \(15\)。使用条件概率不难计算得到,如果该买家的估值真的为 \(10\),那么他的期望效用为 \(0\),但如果他的真实估值为 \(100\),那么他的期望效用为 \(-50/3\),因此故意报低价并不有利。
这样的旁注在买家估值独立的情况下是不可能出现的,因为独立情况下的条件概率其实就是原先事件的概率本身,因此不会出现上面诚实与不诚实的情况下买家的期望效用的区别(因为条件概率不会有区别了)。因此在买家估值相关的情况下,我们可以通过设计旁注来设计最优机制:当买家诚实时,我们设计他的期望效用为 \(0\),但是当买家不诚实时,我们设计他的期望效用为负值,从而阻止他不诚实报价。
当然上面我们给出的 \((p,x)\) 有一个弊端,即双方都报低价也是一个纳什均衡。事实上我们可以设计另一个同样最优的机制来解决这一问题:
\(p\) 保持之前的设定。一个自然的问题是,是否存在不这么“诡异”的机制是最优的呢?答案是不存在,事实上我们可以将上面的例子中的最优机制设计问题描述为一个线性规划,如果我们添加“卖家不向买家支付”这一约束,那么最优解对应的卖家收益为 \(66\dfrac{2}{3}\),而去除这一约束的最优机制(即前面给出的机制)的期望效用为 \(70\)。