跳转至

凸优化基础知识

凸集与分离超平面定理

凸集

回忆基础知识，集合 \(X \subseteq \mathbb{R}^n\) 是凸（convex）的，当且仅当对于任意的 \(x, y \in X\) 和 \(0 \leqslant \lambda \leqslant 1\)，都有 \(\lambda x + (1 - \lambda) y \in X\)。令 \(x^0,x^1,\ldots,x^k \in \mathbb{R}^n\)，则 \(x^0,x^1,\ldots,x^k\) 的凸包（convex hull）\(\text{conv}(x^0,x^1,\ldots,x^k)\) 定义为

\[ \text{conv}(x^0,x^1,\ldots,x^k) = \left\{ \sum_{i=0}^k \lambda_i x^i \mid \lambda_i \geqslant 0, \sum\limits_{i=0}^k \lambda_i = 1 \right\} \]

其中 \(\sum\limits_{i=0}^k \lambda_i x^i\) 称为 \(x^0,x^1,\ldots,x^k\) 的凸组合。凸包是凸集的一个重要概念，不难验证它是包含 \(x^0,x^1,\ldots,x^k\) 的最小凸集。

令 \(X \subseteq \mathbb{R}^n\) 是一个凸集，向量 \(x \in X\) 是 \(X\) 的一个极端点（extreme point），当且仅当对于任意的 \(y, z \in X\) 和 \(0 < \lambda < 1\)，都有 \(x \neq \lambda y + (1 - \lambda) z\)。即极端点无法被表达为两个不同的点的凸组合，或者说不存在一个开区间包含 \(x\) 且完全包含在 \(X\) 中。下图描述了圆盘和正方形的极端点，实际上非常符合我们的直观：圆盘的极端点就是整个最外圈的圆，正方形的极端点就是正方形的顶点。

有一个基本的结果是，如果 \(X\) 是一个闭集，那么对每个点 \(x \notin X\)，至少存在一个点 \(y\) 距离 \(x\) 最近。我们将要证明的是，如果 \(X\) 是闭凸集，这一最近的点是唯一的：

定理

令 \(X \subseteq \mathbb{R}^n\) 是一个闭凸集，\(x \in \mathbb{R}^n\) 是一个不在 \(X\) 中的点，则存在唯一的 \(y \in X\)，使得 \(d(x,X) = d(x,y)\)。

证明

首先根据闭集可知至少存在一个点 \(y \in X\)，使得 \(d(x,X) = d(x,y)\)。接下来用反证法，假设存在另一个点 \(z \in X\) 使得 \(d(x,z) = d(x,X)\)，因为 \(X\) 是凸集，\(\dfrac{y+z}{2} \in X\)，我们证明 \(d(x,\dfrac{y+z}{2}) < d(x,y)\) 来得到矛盾（因为 \(y\) 是距离 \(x\) 最近的点）。我们可以定义函数 \(D: \mathbb{R} \to \mathbb{R}\) 为

\[\begin{aligned} D(\alpha) &= d(x,\alpha y + (1 - \alpha) z) \\ &= \sum\limits_{i=1}^n (x_i - \alpha y_i - (1 - \alpha) z_i)^2 \\ &= \sum\limits_{i=1}^n (x_i - z_i - \alpha (y_i - z_i))^2 \end{aligned}\]

事实上这是关于 \(\alpha\) 的一个二次函数，并且 \(\alpha^2\) 的系数是正数，根据 \(D(0) = D(1)\) 可知 \(D(\alpha)\) 在 \((0,1)\) 内取得最小值，实际上根据对称性就是 \(D(1/2)\)，因此 \(d(x,\dfrac{y+z}{2}) < d(x,y)\)，得到矛盾。

下面是一个无关的结论，放在这里只是因为想起来有这么个结果，然后也为了提醒一下我自己学过这一结论：

一个补充的结论

设 \(X\) 是一个闭集，\(Y\) 是一个集合，满足 \(X \cap Y = \varnothing\)，那么

  1. 若 \(Y\) 是紧集，则 \(d(X,Y) > 0\)；
  2. 若 \(Y\) 是闭集，则 \(d(X,Y)\) 可能等于 \(0\)。

补充结论的证明

  1. 因为 \(X \cap Y = \varnothing\)，因此对于任意的 \(y \in Y\)，都存在 \(\delta_y\) 使得 \(d(y,X) > 2\delta_y\)，故 \(B(y,\delta_y) \cap X = \varnothing\)。因为 \(Y\) 是紧集，因此根据有限覆盖定理，存在有限个 \(y_1,y_2,\ldots,y_k\) 使得 \(Y \subseteq \bigcup\limits_{i=1}^k B(y_i,\delta_{y_i})\)。令 \(\delta = \min\{\delta_{y_1},\delta_{y_2},\ldots,\delta_{y_k}\}\)，则 \(\forall x \in X, y \in Y\)，都存在一个 \(i\) 使得 \(y \in B(y_i,\delta_{y_i})\)，即 \(|y - y_i| \leqslant \delta_{y_i}\)，因此 \(|x - y| \geqslant |x - y_i| - |y - y_i| > 2\delta_{y_i} - \delta_{y_i} = \delta_{y_i} \geqslant \delta\)，即 \(d(X,Y) \geqslant \delta > 0\)。
  2. 只需注意到 \(y = 1/x\) 的函数曲线与 \(x\) 轴都是闭集，但它们之间的距离为 \(0\) 即可。

分离超平面定理

在应用中有一个非常常用的结论，即分离超平面定理（Separating Hyperplane Theorem）。为了描述这一定理，我们首先需要定义一些术语：

超平面定义

\(\mathbb{R}^n\) 中的一个超平面（hyperplane） \(H(\alpha,\beta)\) 可以由一个法向量 \(\alpha \in \mathbb{R}^n\) 和一个标量（称为截距） \(\beta \in \mathbb{R}\) 确定，即

\[ H(\alpha,\beta) = \{ x \in \mathbb{R}^n \mid \langle \alpha,x \rangle = \beta \} \]

其中 \(\langle \alpha,x \rangle = \alpha_1 x_1 + \alpha_2 x_2 + \cdots + \alpha_n x_n\) 是 \(\alpha\) 和 \(x\) 的内积。我们记 \(H^+(\alpha,\beta) = \{ x \in \mathbb{R}^n \mid \langle \alpha,x \rangle \geqslant \beta \}\) 和 \(H^-(\alpha,\beta) = \{ x \in \mathbb{R}^n \mid \langle \alpha,x \rangle \leqslant \beta \}\) 分别为超平面 \(H(\alpha,\beta)\) 的半空间（half-space）。

事实上我们可以将超平面的定义 \(\alpha_1 x_1 + \alpha_2 x_2 + \cdots + \alpha_n x_n = \beta\) 视为用一个线性约束得到了一个 \(n-1\) 维的“平面”。\(\alpha\) 被称为法向量的原因是，如果我们任取 \(x_1,x_2 \in H(\alpha,\beta)\)，则有 \(\langle \alpha,x_1 \rangle = \langle \alpha,x_2 \rangle = \beta\)，因此 \(\langle \alpha,x_1 \rangle - \langle \alpha,x_2 \rangle = 0\)，即 \(\langle \alpha,x_1 - x_2 \rangle = 0\)，这说明 \(\alpha\) 与 \(H(\alpha,\beta)\) 上的任意向量正交。

一个超平面将一个集合和一个点分离，条件是：这个集合被包含在超平面的一个半空间中，而这个点在另一个半空间中。这一定义的形式化描述如下：

分离的定义

令 \(S \subseteq \mathbb{R}^n\) 是一个集合，\(x \in \mathbb{R}^n\) 是一个向量。超平面 \(H(\alpha,\beta)\) 将 \(S\) 和 \(x\) 分开，条件是

  1. \(S \subseteq H^+(\alpha,\beta)\) 且 \(x \in H^-(\alpha,\beta)\)，或者
  2. \(S \subseteq H^-(\alpha,\beta)\) 且 \(x \in H^+(\alpha,\beta)\)。

如果 \(x\) 和 \(S\) 的分离是严格的，如果

  1. \(S \subseteq H^+(\alpha,\beta)\backslash H(\alpha,\beta)\) 且 \(x \in H^-(\alpha,\beta)\backslash H(\alpha,\beta)\)，或者
  2. \(S \subseteq H^-(\alpha,\beta)\backslash H(\alpha,\beta)\) 且 \(x \in H^+(\alpha,\beta)\backslash H(\alpha,\beta)\)。

有了上面的定义之后，我们就可以开始描述分离超平面定理了。分离超平面定理说的是，对每个闭凸集以及每个不在那个集合中的每个点，都存在一个超平面将这个集合和这个点严格分离，并且定理还直接给出了如何构建这样一个超平面：

分离超平面定理

令 \(S \subseteq \mathbb{R}^n\) 是一个闭凸集，\(x \in \mathbb{R}^n\) 是一个不在 \(S\) 中的点，\(y\) 是 \(S\) 中距离 \(x\) 最近的点（上一小节的结论表明这样的点存在）。那么超平面 \(H(x-y,\langle x-y,y \rangle)\) 将 \(S\) 和 \(x\) 分离。进一步地，存在超平面将 \(S\) 和 \(x\) 严格分离。

这个定理的几何解释非常直观：我们将 \(x-y\) 作为超平面的法向量是很自然的事情，然后我们设置截距项让超平面过 \(y\) 点，这样因为 \(S\) 是闭凸集，所以 \(S\) 中的所有点都在 \(y\) 的一侧，而 \(x\) 在 \(y\) 的另一侧，因此这个超平面将 \(S\) 和 \(x\) 分开。如果我们进一步要求严格分离，那么我们可以稍微调整截距项，使得超平面不经过 \(y\) 点，让平面在 \(x,y\) 两点之间即可。下图给出了一个世纪的例子供读者体会。

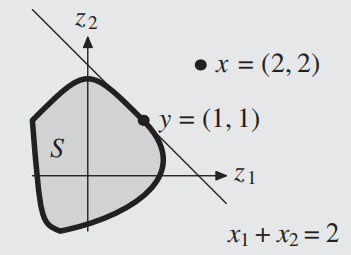
分离超平面定理的证明

我们直接根据定义证明超平面 \(H(x-y,\langle x-y,y \rangle)\) 将 \(S\) 和 \(x\) 分离即可，严格分离前面的分析已经得到了方法。

  1. 证明 \(x \in H^+(x-y,\langle x-y,y \rangle)\)：这等价于 \(\langle x-y,x \rangle \geqslant \langle x-y,y \rangle\)，即 \(\langle x-y,x-y \rangle \geqslant 0\)，根据内积的正定性这是显然的。事实上因为 \(d(x,S) > 0\) 因此 \(x \neq y\)，所以这个不等式是严格的，因此事实上有 \(x \in H^+(x-y,\langle x-y,y \rangle)\backslash H(x-y,\langle x-y,y \rangle)\)。
  2. 证明 \(S \subseteq H^-(x-y,\langle x-y,y \rangle)\)：这等价于对于任意的 \(z \in S\)，都有 \(\langle x-y,z \rangle \leqslant \langle x-y,y \rangle\)，即 \(\langle x-y,z-y \rangle \leqslant 0\)。因为 \(S\) 是凸的，所以 \(\lambda z + (1 - \lambda) y \in S\) 对于任意的 \(\lambda \in [0,1]\) 成立。因为 \(y\) 是 \(S\) 内与 \(S\) 最接近的点，所以 \(d(x,y) \leqslant d(x,\lambda z + (1 - \lambda) y)\)，根据 \(d(x,y) = \sqrt{\langle x-y,x-y \rangle}\) 和内积的性质，我们有
\[\begin{aligned} \langle x-y,x-y \rangle &\leqslant \langle x - (1 - \lambda) y - \lambda z, x - (1 - \lambda) y - \lambda z \rangle \\ &= \langle x-y,x-y \rangle - 2\lambda \langle x-y,z-y \rangle + \lambda^2 \langle z-y,z-y \rangle \\ \end{aligned}\]

消去重复项，得到对于任意的 \(\lambda \in [0,1]\)，都有 \(0 \leqslant -2\lambda \langle x-y,z-y \rangle + \lambda^2 \langle z-y,z-y \rangle\)，\(\lambda \in (0,1]\) 时可以得到 \(0 \leqslant -2\langle x-y,z-y \rangle + \lambda \langle z-y,z-y \rangle\)，令 \(\lambda \to 0\) 即可得到 \(0 \leqslant -2\langle x-y,z-y \rangle\)，即 \(\langle x-y,z-y \rangle \leqslant 0\)，因此 \(S \subseteq H^-(x-y,\langle x-y,y \rangle)\)。

事实上分离超平面定理有一个很自然的推广：

分离超平面定理的推广

令 \(X,Y \in \mathbb{R}^n\) 是两个闭凸集，如果 \(X \cap Y = \varnothing\)，则存在超平面 \(H(\alpha,\beta)\) 将 \(X\) 与 \(Y\) 分离。

证明思路非常简单，因为两个集合都是闭集，因此最小化两个集合之间距离的点都可以取到，设为 \(x \in X,y \in Y\)，然后根据分离超平面定理得到分离 \(x\) 和 \(Y\)，以及分离 \(y\) 和 \(X\) 的两个超平面，然后取两个超平面之间的平面就是分离两个集合的超平面。需要注意的是，两个闭凸集之间不一定可以严格分离，这一点可以从两个不相交的闭集距离可以等于 \(0\) 看出来。

单纯形

仿射无关性

接下来我们需要介绍一些有关于单纯形的基本知识，为了引入单纯形，我们需要首先介绍仿射无关性的概念。

仿射无关的定义

\(\mathbb{R}^n\) 中的向量 \(x^0,x^1,\cdots,x^k\) 是仿射无关的，条件是： \(\mathbb{R}\) 内未知数为 \((\alpha^l)_{l=0}^k\) 的如下方程：

\[\begin{align} \sum\limits_{l=0}^k \alpha^l x^l &= 0 \\ \sum\limits_{l=0}^k \alpha^l &= 0 \end{align}\]

只有唯一解 \(\alpha^0 = \alpha^1 = \cdots = \alpha^k = 0\)。如果这一条件不满足，则称向量 \(x^0,x^1,\cdots,x^k\) 是仿射相关的。

这一定义并不直观，但我们可以联系一个相关的概念：线性相关来讨论这一定义的直观：考虑 \(\mathbb{R}^3\) 中的三个向量 \(x^0,x^1,x^2\)，它们线性相关的含义是，其中一个向量能被另外两个向量线性表示（等价的，可以写成线性组合的形式）。那么仿射相关的含义其实是，其中一个向量可以写成另外两个向量的仿射组合（仿射组合（affine combination）指组合的系数求和为 \(1\)），例如可以有

\[ x^0 = t x^1 + (1 - t) x^2 \]

移项可得 \(x^0 - tx^1 + (t-1) x^2 = 0\)，这三个向量前面的系数为 \((1,-t,t-1)\)，因此不全为 \(0\) 但求和为 \(0\)（其实系数求和为 \(0\) 就是因为等号左侧 \(x^0\) 前的系数是 \(1\)，而等号右侧因为是仿射组合所以系数求和为 \(1\)，移项之后就求和为 \(0\) 了，由此可以看出仿射组合的直观与前面定义的等价性），根据前面的定义可知的确是仿射相关的。那么对应的，仿射无关的含义就是任何向量都不能被其它向量仿射表示。

仿射无关的几何直观也是自然的，事实上三个点仿射无关，也就是任何一个点不能被其余两个仿射表示，注意两个点的仿射组合其实就是两点所在的直线，因此只要平面上三点不共线就是仿射无关的。空间中四个点的仿射无关我们需要考察任意三个点的仿射组合是什么：实际上就是三个点所在的平面！因此只要四点不共面即可实现仿射无关。

由此我们也发现了仿射无关和线性无关尽管非常相似，但并不是一个概念。平面上三点不共线就可以仿射无关，但考虑 \((1,0),(0,1),(1,1)\) 这三个点，它们是线性相关的。反之，根据线性无关的定义可以直接推出仿射无关，因此仿射无关是一个更弱的约束。更具体地，我们有如下定理：

仿射相关与线性无关

考虑 \(\mathbb{R}^n\) 中的向量组 \(S = \{x^0,x^1,\cdots,x^k\}(k \geqslant 2)\)，下列说法等价：

  1. \(S\) 仿射相关；
  2. \(S\) 中的一个点可以被其余点的仿射组合表示；
  3. \(x^1-x^0,x^2-x^0,\cdots,x^k-x^0\) 线性相关。

实际上这里的 1 和 2 的等价性就是前面定义的直观解释，这表明，线性无关与仿射无关等相关概念其实都可以平移理解第三条一方面很容易让我们回想起非齐次线性方程组 \(AX=b\) 的解的性质，实际上 \(AX=b\) 的解可以视为 \(\{X_0,X_0+X_1,\cdots,X_0+X_p\}\) 的全体仿射组合的结果，其中 \(X_0\) 是 \(AX=b\) 的一个特解，\(X_1,\cdots,X_p\) 是 \(AX=0\) 的基础解系；另一方面，1 和 3 的等价性表明，\(S\) 仿射无关等价于 \(x^1-x^0,x^2-x^0,\cdots,x^k-x^0\) 线性无关，因此 \(\mathbb{R}^n\) 中可能存在 \(n+1\) 个仿射无关向量，但是不存在 \(n+2\) 个仿射无关向量，否则这样作差会得到 \(n+1\) 个线性无关向量：

仿射相关与线性无关的推论

\(\mathbb{R}^n\) 中可能存在 \(n+1\) 个仿射无关向量，但是不存在 \(n+2\) 个仿射无关向量。

重心坐标系统

我们知道，\(\mathbb{R}^n\) 中的 \(n\) 个线性无关向量构成一组基，因此空间中任一向量都可以在基下唯一表示，那么类似的，一组仿射无关向量 \(x^0,x^1,\cdots,x^k\) 的全体仿射组合 \(\text{aff}\{x^0,x^1,\cdots,x^k\}\) 中的全体向量也应当可以在 \(x^0,x^1,\cdots,x^k\) 下有唯一的仿射表示（证明与线性空间类似，略去）.

在线性空间中，张成整个空间的一组线性无关向量称为一组基，这组基相当于给这个线性空间加了一个坐标系。在仿射组合中，每个向量的唯一仿射表示的系数也构成一个坐标，我们称之为重心坐标（barycentric coordinates），这个坐标系统也就称为重心坐标系统。

重心坐标的含义实际上很明确，我们回忆 \(n\) 个质量分别为 \(m_1,m_2,\cdots,m_n\) 的质点在空间中的重心坐标，假设质点的位置分别为 \(\pmb{r}_1,\pmb{r}_2,\cdots,\pmb{r}_n\)，那么重心坐标就是

\[ \pmb{r} = \dfrac{m_1\pmb{r}_1 + m_2\pmb{r}_2 + \cdots + m_n\pmb{r}_n}{m_1 + m_2 + \cdots + m_n} \]

等号右侧事实上就是一个仿射组合，因此“重心”这一名词是很直观的。

单纯形

有了前面的基础，我们可以定义单纯形（simplex）的概念了。事实上单纯形是最简单的一类凸集，因此我们对凸集的很多研究可以从单纯形入手，然后进一步推广到一般凸集：

单纯形的定义

集合 \(S \subseteq \mathbb{R}^n\) 称为一个 \(k\) 维单纯形，如果 \(S\) 是由 \(k+1\) 个仿射无关的向量 \(x^0,x^1,\cdots,x^k\) 张成的凸包，即

\[ S = \text{conv}(x^0,x^1,\cdots,x^k) = \left\{ \sum_{i=0}^k \lambda_i x^i \mid \lambda_i \geqslant 0, \sum\limits_{i=0}^k \lambda_i = 1 \right\} \]

我们将上述单纯形记作 \(\langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\)。显然，一个单纯形是一个凸紧集，零维单纯形是一个单点集合，一维单纯形就是一个闭区间，二维单纯形是一个三角形，三维单纯形是一个四面体，等等。并且单纯形的极端点根据定义就是 \(x^0,x^1,\cdots,x^k\)。下面这一定理是重心坐标系统的自然推论，表明单纯形内的每一个向量都可以被表达为单纯形极端点的凸组合：

凸组合

令 \(x^0,x^1,\cdots,x^k\) 是 \(\mathbb{R}^n\) 中 \(k+1\) 个仿射无关的向量，令 \(y \in \langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\)，那么 \(y\) 可以表达为 \(x^0,x^1,\cdots,x^k\) 的唯一凸组合。换言之，\(\mathbb{R}\) 中未知数为 \((\alpha^l)_{l=0}^k\) 的如下方程有唯一解：

\[\begin{align} \sum\limits_{l=0}^k \alpha^l x^l &= y \\ \sum\limits_{l=0}^k \alpha^l &= 1 \\ \alpha^l &\geqslant 0, \forall l = 0,1,\cdots,k \end{align}\]

用重心坐标系统解释就是，如果在每个点 \(x^l\) 处放置一个质量为 \(\alpha^l\) 的质点，所有质点质量之和为 \(1\)，那么这些质点的重心就是 \(y\)。

有一个显然的事实是，仿射无关向量组的子集仍然是仿射无关的，因此我们还可以有下面的结论以及相关的定义：

单纯形的面

令 \(S = \langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\) 是 \(\mathbb{R}^n\) 中的一个 \(k\) 维单纯形，那么对每个集合 \(\{x^{l_0},\cdots,x^{l_t}\} \subseteq \langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\)，\(\{x^{l_0},\cdots,x^{l_t}\}\) 张成的凸包称为 \(S\) 的一个 \(t\) 维面（face），事实上也是一个 \(t\) 维子单纯形（subsimplex）。特别地，\(S\) 的每个极端点都是 \(S\) 的一个 \(0\) 维面，\(S\) 本身是一个 \(k\) 维面。

这一定义非常直观，例如一个四面体的所有面就是所有顶点、所有边、所有三角面，以及整个四面体本身。进一步地，我们定义单纯形的边界：

单纯形的边界

令 \(S = \langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\) 是 \(\mathbb{R}^n\) 中的一个 \(k\) 维单纯形，\(S\) 的边界（boundary）定义为 \(S\) 的所有 \(k-1\) 维子单纯形（或 \(k-1\) 维面）的并集，即

\[ \partial S = \bigcup\limits_{l=0}^k \langle \langle x^0,x^1,\cdots,x^{l-1},x^{l+1},\cdots,x^k \rangle \rangle \]

这一定义也是很自然的，例如一个三角形的边界就是三角形的三条边，一个四面体的边界就是四面体的所有面。有了如上定义的基础，我们将要定义一个比较复杂的概念，即单纯形的划分，这一定义是博弈论中要介绍的斯佩纳引理的讨论基础。

单纯形的划分

令 \(S \subseteq \mathbb{R}^n\) 是一个 \(k\) 维单纯形，\(S\) 的一个划分（partition）是 \(\mathbb{R}^n\) 中的一组单纯形 \(\mathcal{T} = \{T_1,T_2,\cdots,T_M\}\)，满足

  1. \(\bigcup\limits_{m=1}^M T_m = S\)：即划分的所有单纯形的并集是整个单纯形 \(S\)；
  2. 对每个 \(0 \leqslant j \leqslant m \leqslant M\)，交集 \(T_j \cap T_m\) 要么是空集，要么 \(T_j\) 和 \(T_m\) 共同的面；
  3. 如果 \(T\) 是 \(\mathcal{T}\) 中的一个单纯形，那么 \(T\) 的所有面也是 \(\mathcal{T}\) 中的单纯形；
  4. 如果 \(T\) 是 \(\mathcal{T}\) 中的一个 \(l\) 维单纯形（\(l < k\)），那么它被包含在 \(\mathcal{T}\) 中的一个 \(l+1\) 维单纯形内。

看起来这个定义非常抽象，的确如此，其中第一、第二条看起来还非常正常，第三第四条就有些摸不着头脑了。事实上第三条想表达的就是 \(\mathcal{T}\) 中任何单纯形的子单纯形也在 \(\mathcal{T}\) 中，第四条则是说 \(\mathcal{T}\) 中低维的单纯形都包含在一个高维单纯形中。其实简单来说都是在规定这个集合需要满足的特点，熟悉拓扑公理化定义的应该也可以接受这样抽象的定义。

当然接受抽象定义之后我们需要看一些例子来理解定义：

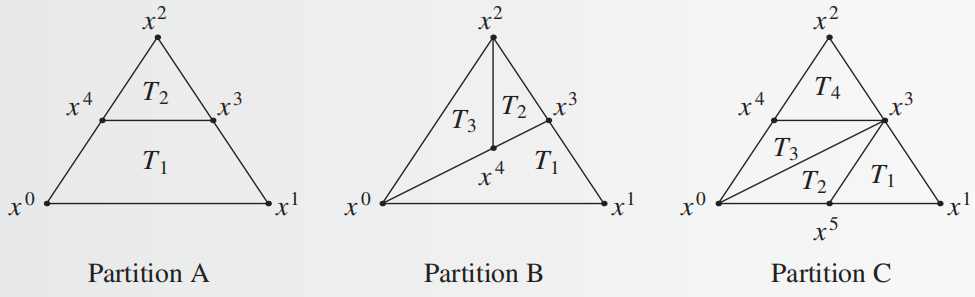
上图中，\(\text{A}\) 显然不是一个合规的划分，因为 \(T_1\) 甚至不是一个单纯形：平面上 \(4\) 个点必定仿射相关，因此四边形并非单纯形。\(\text{B}\) 也不是满足定义的划分，因为 \(T_1\) 和 \(T_2\) 的交集不是 \(T_1\) 的面，只是 \(T_1\) 的面的一部分，\(T_1\) 与 \(T_3\) 同理。\(\text{C}\) 是一个合理的划分，其中 \(\mathcal{T}\) 包含 \(T_1,T_2,T_3,T_4\) 以及它们的所有面。相比之下，\(T_1,T_2,T_3,T_4,T_1 \cup T_2\) 和它们所有的面并不构成划分，因为 \(T_1\) 和 \(T_1 \cup T_2\) 的交集是 \(T_1\)，这不是\(T_1 \cup T_2\) 的一个面。

事实上，根据单纯形划分的定义中第 1、4 两条，我们可以得到结论：\(k\) 维单纯形 \(S\) 等于 \(\mathcal{T}\) 中所有 \(k\) 维单纯形的并集。这一点在上面的 \(\text{C}\) 中也是可以看出来的。

关于单纯形，我们还可以引入一个记号，之后将会用到。对于每个单纯形划分 \(\mathcal{T} = \{T_1,T_2,\cdots,T_M\}\)，我们用 \(Y(\mathcal{T})\) 表示单纯形 \((T_m)_{m=1}^M\) 的所有极端点的集合，例如上图 \(\text{C}\) 中，\(Y(\mathcal{T}) = \{x^0,x^1,x^2,x^3,x^4,x^5\}\)。等价地说，每个 \(T_m \in \mathcal{T}\) 都是 \(Y(\mathcal{T})\) 内一些点的凸组合。

最后我们用一个很难证明（因此这里不给出证明）的定理来结束我们对单纯形划分的讨论，它将会在博弈论中要介绍的斯佩纳引理的证明中用到，事实上前面的知识很大程度上就是为了引入斯佩纳引理做准备的。

划分的性质

令 \(S = \langle \langle x^0,x^1,\cdots,x^k \rangle \rangle\) 是 \(\mathbb{R}^n\) 中的一个 \(k\) 维单纯形，\(\mathcal{T}\) 是 \(S\) 的一个划分，\(T \in \mathcal{T}\) 是 \(\mathcal{T}\) 中的一个 \(k-1\) 维单纯形。如果 \(T\) 在 \(S\) 的边界内，那么 \(T\) 被包含在 \(\mathcal{T}\) 内的唯一一个 \(k\) 维单纯形内；如果 \(T\) 不在 \(S\) 的边界内，那么 \(T\) 被包含在 \(\mathcal{T}\) 内的两个 \(k\) 维单纯形内。

例如上图的 \(\text{C}\)，一维单纯形 \(\langle \langle x^1,x^3 \rangle \rangle\) 在 \(S\) 的边界内，它的确被包含在 \(\mathcal{T}\) 内的唯一一个二维单纯形 \(T_1\) 内；而 \(\langle \langle x^3,x^5 \rangle \rangle\) 不在边界内，它也的确被包含在 \(\mathcal{T}\) 内的两个二维单纯形 \(T_1,T_2\) 内。由此我们可以感受到这一定理是非常直观的，边界上的就在唯一分区中，而内部的就在两个分区中，很符合我们对“划分”的直观，但严格证明技术性很强，因此略去。