计算机系统——从小白学起

Hello，欢迎来到计算机系统——从小白学起！这是一本致力于从零基础开始学习计算机系统知识，贯通数字逻辑设计、计算机组成、计算机体系结构以及操作系统四门经典的计算机系统课程的书，我们希望在这本书中实现以下与其他教科书不一样的特性：

很多中文教科书对于初学者而言，文字描述晦涩难懂，更像是百科式的知识点罗列，细节描述也十分含糊，整体思路也不够清晰，本书希望做到语言描述清晰易懂，思路更加适合于初学者从零开始的接受能力，也更适合于构建完整的知识体系；
国外教科书，特别是最经典的几本教材厚度足够劝退，并且其中语言描述有时略显冗余，全书通读性价比较低，并且其中许多重点或是细节的描述更像是一直在兜圈子，讲了很多，描述却仍旧十分含糊。本书希望在保证讲解清晰的同时语言精简，同时知识编排也更有条理；
作为浙江大学信息安全系系统贯通课程的亲历者，笔者希望追随并扩展这一成功的试验，将四门计算机系统课程贯通，而非遵循传统的课程拆散，相互之间出现大量冗余内容的同时却仍然有许多内容都讲解不够深入的问题，从而构建完整的计算机系统知识与实验体系。

项目协作

非常欢迎大家参与到这一项目的构建中。由于作者精力与能力有限，很难高质量地完成本书的所有内容，因此非常需要更多对这一项目有热情的人参与进来。

本项目目前使用 mdbook 框架，在 GitHub 上有同步的仓库 yhwu-is/Computer-System-Start-From-a-Newbie 欢迎各位评论，也欢迎加入我们。

Part0 初识计算机系统

Chapter00 初识计算机系统

作为开头，本节将带你解剖一只麻雀——你的计算机的组成。阅读完本节，你应当对计算机系统的研究内容有一个整体的印象。

0.1 从你的电脑讲起

计算机系统由两个个部分组成：

硬件
软件

硬件

计算机的硬件可以分为三大类：中央处理单元、主存储器和输入/输出子系统。

中央处理单元

在大多数体系结构中，CPU 有三个组成部分：

算术逻辑单元（ALU）：执行逻辑、位移和算术运算
控制单元：发送到其他子系统的信号，控制各个子系统的操作
寄存器组：存放零时数据的高速独立的存储单元

主存储器

主存储器是存储单元的集合。每个存储单元都有唯一的标识，称为地址。数据以称为字的位组的形式在内存中传入和传出。常见的字的大小为 32 位或 64 位。8 位称为 1 字节。

计算机用户需要很多存储器，尤其是速度快且价格低廉的存储器。然而存取速度快的存储器通常都不便宜，折中的办法是采用存储器层次结构：用较快的存储器存储经常访问的数据，用较慢的存储器存储不常访问的数据。

输入/输出子系统

I/O 子系统有如下分类，在此不做展开叙述：

非存储设备
- 键盘和监视器
- 打印机
存储设备
- 磁介质：磁盘、磁带
- 光存储：CD-ROM、DVD

子系统的互连

CPU 与存储器的连接

CPU 和存储器间通常由称为总线的三组线路连接在一起，分别是：数据总线、地址总线和控制总线。

I/O 设备的互连

输入/输出设备不能直接与总线相连，因为输入/输出设备的本质（机电、磁、光学设备）与 CPU 和内存（电子设备）不同，而且速度要慢得多。它们通过输入/输出控制器连接到总线上。

SCSI、火线、USB 和 HDMI 等都是控制器，它们清除了 I/O 设备与 CPU 和内存本质上的障碍。

串行控制器：只有一根数据线连接到设备上
并行控制器：有数根数据线连接到设备商，一次能同时传输多个位

软件

计算机软件分为两大类：操作系统和应用程序。计算机系统的研究对象是操作系统。

什么是操作系统

操作系统是计算机硬件和用户之间的接口，它使得其他程序能更加方便有效地运行，并能方便地对计算机硬件和软件资源进行访问。

操作系统概述

现代操作系统至少具有4种功能：

内存管理
进程管理
设备管理
文件管理

此外，还具有一个用户界面（或命令解释程序），负责系统与外界的通信。

主流操作系统

计算机用户熟悉的操作系统有三种：UNIX、Linux 和 Windows。

UNIX 和 Linux 类似。它们是多用户、多进程、可移植的操作系统。UNIX 由四部分构成：内核、命令解释器、一组标准工具和应用程序。Linux 由三部分构成：内核、系统工具和系统库。
Windows 是面向对象的、多层的操作系统，包括硬件抽象层、执行层和环境子系统层。

看完 0.1 节的内容后，想必你已经初步了解了计算机的“组成”与“构成”。那么接下来一个很自然的问题便是，计算机是如何发展到今天的形式，其中的设计原理又在何处呢？相信本节关于历史发展的介绍会给你比较满意的答案。

0.2 历史的观点看计算机系统

0.2.1 故事的开始——探索机器解决问题的方案

0.2.1.1 初步的尝试——从非自动化计算工具开始

看到 0.2.1 节的标题，你或许会想起已有两千多年历史的算盘（如图 1-1）。的确，这一中国古人智慧的结晶在是可以帮助人简化并加快计算的步骤的“计算工具”。然而，“计算机器”是需要非人力方式实现自动化操作的，算盘在这一方面则无法实现了。

将目光看向古代西方文明。1900 年，潜水员在安迪基提腊岛附近发现一个青铜器具，上有齿轮和刻度盘，是公元前 65 年左右古希腊人用来计算天体运行的工具。意大利的庞培城，公元 79 年被火山岩浆湮没，直到 20 世纪才大白于世，在遗物中发现罗马时代的比例规。这些都是古代计算工具的实物。

图 1-1. 算盘——我国古代常用的计算工具

或许与文艺复兴的思潮有关，欧洲人在这时开始逐渐深入了对于机器解决问题方案的探索。大量机械重复的计算问题困扰着人们，但同时也成为了人们发明计算机器解决计算问题的一大动力。

首先需要介绍的，也并非完全自动的计算机器——计算尺。这是一种类似于算盘，但是能实现更多功能（如求根、指对数、三角函数等）的计算工具，但是也缺少了自动化的能力。

计算尺的思想来源于约翰·纳皮尔——对数的发明者。对数发明以后，乘除运算可以化为加减运算，利用这一特点，可制成对数计算尺，其使用示例如图 1-2 所示。

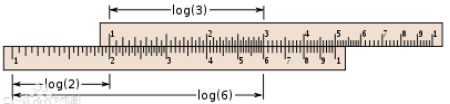
图 1-2. 对数计算尺示例

约翰·纳皮尔（John Napier，1550-1617），苏格兰数学家、神学家，对数的发明者。那时天文学家 Tycho Brahe（第谷，1546～1601）等人做了很多的观察，需要很多的计算，而且要算几个数的连乘，因此苦不堪言。1594 年，纳皮尔为了寻求一种球面三角计算的简便方法，运用了独特的方法构造出对数方法。1614 年 6 月在爱丁堡出版的第一本对数专著《奇妙的对数表的描述》（"Mirifici logarithmorum canonis descriptio"）中阐明了对数原理，后人称为纳皮尔对数：Nap logX。

最早将纳皮尔的理论转化为实物的是英国的 E·冈特，他设计的计算尺以后经多次的改进，才成为现代的计算尺。几次大的进步是：1632 年 W·奥特雷德发明有滑尺的计算尺，同时造出圆形计算尺。1652 年 R·比萨克、1657 年 S·帕特里奇制造有固定尺身和滑尺的计算尺。1850 年法国的曼南将游标装在尺上，被广泛采用。在计算尺的发展历程中，算尺的形状也从直尺多样化为圆尺、柱状算尺，“倒数刻度”等其他刻度被逐步引入，产生了“多相”算尺。除此之外，除了乘除法计算外的求根式、指对数、三角函数等运算也逐步引入计算尺的功能。

20 世纪 50-60 年代，计算尺是工程师身份的象征，如同显微镜代表医学行业一样。有些工程系的学生和工程师常把10-英寸算尺别在皮带上，或者把一把10-或20-英寸算尺安放在家中或办公室里做精确运算用。然而，非自动化的局限性还是使得计算尺逐渐淡出历史舞台，袖珍科学计算器（即带有三角和对数函数的计算器）的诞生为计算尺敲响了最后的丧钟。

0.2.1.2 自动化计算工具的开端——机械计算器的设计

算盘、计算尺等计算工具终究离不开人的控制与调节。如何将输入送入机器后，能不需要人的调控便可以获得需要的输出，这才真正实现了机器解决问题的理想。

令人兴奋的是，一个天才少年——布莱士·帕斯卡的出现打开了自动化计算工具设计的大门。为了帮助父亲计算大量的税率税款，他想到了要为父亲制造一台会计算的机器。他根据数的十进位制，通过齿轮的比来解决进位问题——低位的齿轮每转动 10 圈，高位上的齿轮只转动一圈，并采用精密的机械原理解决计算和自动进位的问题。终于，在1642 年，19 岁的帕斯卡获得了成功，他称这架小小的机器为“加法器”，尽管这台机械式计算机的设计原理完全正确，可它在机械方面还有不少缺陷。

布莱士·帕斯卡（Blaise Pascal，1623-1662），法国数学家、物理学家、哲学家、散文家。他 16 岁时发现著名的帕斯卡六边形定理，17 岁时写成的《圆锥曲线论》是自希腊阿波罗尼奥斯（Apollonius of Perga）以来圆锥曲线论的最大进步。1642 年，他设计并制作了一台能自动进位的加减法计算装置，被称为是世界上第一台数字计算器。1654 年他开始研究几个方面的数学问题，在无穷小分析上深入探讨了不可分原理，得出求不同曲线所围面积和重心的一般方法，并以积分学的原理解决了摆线问题，于 1658 年完成《论摆线》。他的论文手稿对莱布尼茨（Gottfried Leibniz）建立微积分学有很大启发。在研究二项式系数性质时，给出的二项式系数展开后人称为“帕斯卡三角形”。他还制作了水银气压计，写了液体平衡、空气的重量和密度等方向的论文。自 1655 年隐居修道院，写下《思想录》（1658）等经典著作。

经过努力，帕斯卡又制成了一台机械式计算机。这台机械式计算机像一个盒子，外壳用黄铜制成。它长 20 英寸、宽 4 英寸、高 3 英寸。机器顶部是一块黄铜板，上面有一排圆孔，通过它可以看见底下的圆环。孔数和圆环数为 8 个，每个圆环可以围绕自己的圆心旋转。圆环上有很多长齿。右面第一个圆环有 12 个齿，第二个有 20 个齿，而其余各有 10 个。由于设计目的是为算账用的，因此这些齿适合当时法国零钱的换算：1 利维尔＝20 苏；1 苏＝12 尖野。自然，所有其他的圆环都可以以苏为单位处理货币，也可以处理数据。

图 1-3. 帕斯卡制成的机械计算机

这种机器开始只能够做 6 位加法和减法，做乘法时必须用连加的方法；做除法时，也只能用连减的方法。而且使用时需用一个小钥匙拨动一下，方可计算；每次计算完毕，都必须复原到零位，下次方可计算。然而，即使只做加法，也有个“逢十进一”的进位问题。帕斯卡采用了一种小爪子式的棘轮装置。当定位齿轮朝 9 转动时，棘爪便逐渐升高；一旦齿轮转到 0，棘爪就“咔嚓”一声跌落下来，推动十位数的齿轮前进一档。

帕斯卡去世十年后，德国数学家莱布尼茨发现了一篇由帕斯卡亲自撰写的“加法器”论文。这勾起了他强烈的发明欲望，决心把这种机器的功能扩大为乘除运算。他在帕斯卡加、减法机械计算机的基础上进行改进，发明了一款更先进的计算器。

戈特弗里德·威廉·莱布尼茨（Gottfried Wilhelm Leibniz，1646－1716），德国哲学家、数学家，是历史上少见的通才，被誉为十七世纪的亚里士多德。他本人是一名律师，经常往返于各大城镇，他许多的公式都是在颠簸的马车上完成的，他也自称具有男爵的贵族身份。

莱布尼茨在数学史和哲学史上都占有重要地位。在数学上，他和艾萨克·牛顿先后独立发现了微积分，而且他所使用的微积分的数学符号被更广泛的使用。莱布尼茨还发现并完善了二进制。在哲学上，莱布尼茨的乐观主义最为著名，他和笛卡尔、巴鲁赫·斯宾诺莎被认为是十七世纪三位最伟大的理性主义哲学家。

莱布尼茨发明的机器叫“乘法器”，该机器长约 67 厘米，图1-4展示了其外部整体构造与内部设计细节。这款计算器设有一个镶有 9 个不同长度齿轮的圆柱，整体由两个部分组成：第一部分是固定的，用于加减法，与帕斯卡先前设计的加法机基本一致；第二部分用于乘除法，这部分是他专门设计的乘法器和除法器，由两排齿轮构成（被乘数轮与乘数轮），这是莱布尼茨首创的。这架计算机中的许多装置成为后来的技术标准，称为“莱布尼茨轮”。我们主要关心乘、除法器部分。它由两个相连的部分组成：其一是位于后方的可以容纳 16 位十进制数字的累加器，位于前方的第二部分包括一个 8 位数字的输入部分。输入部分有 8 个带旋钮的拨盘，用于设置操作数。输入部分右侧有一个类似电话的拨盘用于设置乘数，前方的曲柄则用于进行计算。运算结果显示在后方累加器的 16 个窗口中。输入部分安装在导轨上，可以沿着累加器部分移动，以改变操作数数字与累加器数字的对齐方式（我们很快便会发现这种设计的目的）。还有一个十进位指示器和一个将机器设置为零的控件。这架机器可进行乘、除法的演算，样机达到了可以进行四则运算的水平。

这台机器的总体设计思路是通过反复加法进行乘法，通过反复减法进行除法。要乘以一位数 0-9，首先将被乘数放在输入部分，然后将旋钮形手写笔插入类似电话的拨盘的相应孔中以设置乘数，然后转动曲柄，乘法器表盘顺时针旋转，机器为每个孔执行一次加法，直到手写笔在表盘顶部停下来。结果出现在累加器窗口中。由此可见，乘以一位数的实现方式是将被乘数累加乘数次。

当乘以一个多位数时，从最低位开始进行一位数乘法操作，当一位计算结束后，我们将输入部分（即乘数）左移——现在你应该理解将输入部分放置在导轨上的原因了，这与竖式乘法的方式完全对应——然后再重复一位数乘法的操作即可。

用减法实现除法的过程也并不难理解。我们将被除数设置在累加器中，除数设置在输入部分中。然后我们移动输入部分直到被除数和除数的左侧数字对齐。转动操作曲柄（与乘法相反，需要将表盘逆时针转动）并重复从累加器中减去除数，直到累加器结果的最高位数字为0。乘数刻度盘上显示的数字就是商的第一个数字。然后将输入部分右移一位（回忆竖式除法的方式）。重复以上减数、移位步骤，得到商的每一位即可。

图 1-4. 莱布尼茨的乘法器

或许大家对加减法次数控制的模块感兴趣，那么我们略微展开说明一下。如图1-5所示，莱布尼茨为计算机增添了一种名叫“步进轮”的装置。步进轮是一个有 9 个齿的长圆柱体，9 个齿长度不同，分布于圆柱表面；旁边另有个小齿轮可以沿着轴向移动，从而可以与步进轮上不同数量的齿啮合。每当小齿轮转动一圈，步进轮可根据它与小齿轮啮合的齿数，转动 1/10 或 2/10 圈……，最多可以转动 9/10 圈，这样就能控制它连续重复地做加减法的次数。

图 1-5. 步进轮

帕斯卡的计算机经由莱布尼茨的改进之后，人们又给它装上电动机以驱动机器工作，成为名符其实的“电动计算机”，并且一直使用到 20 世纪 20 年代才退出舞台。然而，一台仅能实现四则运算的机器无法满足人们对于机器解决更多问题的需求，还需等待更伟大的构想。

0.2.1.3 超前的伟大构想——从巴贝奇的差分机到分析机

莱布尼茨发明乘法器后的一百余年中，人类关于计算机器的设想大多停滞在对于乘法器的改进上。然而，这些越来越精密的仪器却仅仅和加、减、乘、除——简单到不能再简单的基本运算打交道。难道机器只能用来做运算吗？为了解决一个数学问题，人们往往需要将多步运算串联起来，每一次串联不过是将上一步的运算结果直接或经过简单处理后交给下一步而已，而既然运算可以由机器完成，为什么步骤就不可以呢？

伟大的设想仍然来自于社会的背景，1789 年法国大革命后，君主制被推翻，新成立的国民议会大刀阔斧地推行着多方改革，其中一项很重要的工作就是统一全国混乱不堪的度量衡，与此同时，原本的数学用表不再适用，需要重新编制。

表的规模十分庞大，计算结果需要精确到小数点后 14～29 位，工作量的巨大可想而知。这项艰巨的任务落在了数学家加斯帕德·德普罗尼（Gaspard de Prony）肩上，他进行了层次分明的分工，并且要求所有数据至少运算两遍——甚至于要求是不同地点不同方法运算两遍，于是他自信宣称“制作数学用表可以像生产针一样简单”。然而，成表的正确率并不尽如人意。多年以后的英国，巴贝奇和约翰·赫歇尔也承担着类似的制表任务。他深入调研了这位前辈的工作，了解到正确率的保障有多困难。他们尝试了各种减少错误的手段，比如调整纸张和墨水的颜色以提高数字的识别度，比如直接拿现有多个版本的表进行誊抄、比对、让不同人员反复校对，结果却依然不尽人意。

于是巴贝奇意识到：只要是人为的，就没有完美的。他思忖着：人类最容易出错的部分，特别是大量机械重复的计算的部分，可否用机器来代替呢？1822 年 6 月 14 日，巴贝奇向皇家天文学会递交了一篇名为《论机械在天文及数学用表计算中的应用》的论文，差分机的概念正式问世。与论文一起亮相的，是一台简单的原型机——差分机 0 号。英国政府对它很有兴趣，并于次年拨款 1700 英镑，希望巴贝奇能做出实用产品，彻底解决制表难题。

查尔斯·巴贝奇（Charles Babbage，1791.12.26—1871.10.18）是一名英国发明家，科学管理的先驱者，出生于一个富有的银行家的家庭，曾就读于剑桥大学三一学院。

他的贡献主要有以下几点：提出了在科学分析的基础上的可能测定出企业管理的一般原则。设计出世界上第一台计算机——于 1823 年设计出来的世界上第一台计算机小型差数机，虽然没有制成，但其基本原理于 92 年后被应用于巴勒式会计计算机。他还利用计数机来计算工人的工作数量、原材料的利用程度等。他制定了一种“观察制造业的方法”。这种方法同后来别人提出的“作业研究的科学的、系统的方法”非常相似。他进一步发展了亚当·斯密关于劳动分工的利益的思想，分析了分工能提高劳动生产率的原因。

于是巴贝奇开始着手于差分机一号（Difference Engine No.1）的设计。简单来说，差分机就是一台多项式求值机，只要将多项式方程 \(F(x)\) 的前 3 个初始值（如 \(F(0), F(1), F(2)\)）输入到机器里，机器每运转一轮，就能产生出多项式后续的一个值。其计算方法来源于帕斯卡在 1654 年提出的差分思想：\(n\) 次多项式的 \(n\) 次数值差分为同一常数。这句话十分抽象，概括性高，我们用几个例子来详细说明。

给定 \(F(x)=5x+6\)，同时定义差分 \(\Delta F(x) = F(x+1)-F(x)\)，则列出表格如下：

\(x\)	0	1	2	3	4	5	6
\(F(x)\)	6	11	16	21	26	31	36
\(\Delta F(x)\)	5	5	5	5	5	5

表 1-1. \(F(x)=5x+6\) 的差分表

不难发现，对于一次多项式，每个相邻的 \(x\) 所对应的 \(F(x)\) 之差都是一个常数。对于二次多项式呢？以 \(F(x)=x^2+4\) 为例，我们同时定义一阶差分

\[\Delta F_1(x)=F(x+1)-F(x)\]

和二阶差分

\[\Delta F_2(x)=\Delta F_1(x+1)-\Delta F_1(x)\]

列出表格如下：

\(x\)	0	1	2	3	4	5	6
\(F(x)\)	4	5	8	13	20	29	40
\(\Delta F_1(x)\)	1	3	5	7	9	11
\(\Delta F_1(x)\)	2	2	2	2	2

表 1-2. \(F(x)=x^2+4\) 的差分表

我们可以发现，对于二次多项式，每个相邻的 \(x\) 所对应的一阶差分之差（即二阶差分）是一个常数。依此类推，\(n\) 次多项式的 \(n\) 次数值差分为同一常数便可以理解了。

基于这一定理，我们便可以实现差分机的功能。给定差分机以多项式 \(F(x)=x^2+4\) 的初始值\(F(1)=5, F(2)=8, F(3)=13\)，计算得到 \(F(x)\) 的二阶差分为常数 2。我们可以从此处开始往前推算回去，接下来的每一个值，就是将高阶差分和低一阶的对应差分相加，不断重复直至加到原多项式为止。例如求 \(F(4)\) 时，先将第二阶差 2 加上第一阶对应差分 5 得到 7，再将 7 加上 \(F(3)\) 的值 13，就会得到 \(F(4)=20\)。以此类推，求出多项方程式的结果完全只需要用到加法与减法，并且不断重复的特性却很适合机械运算。

差分机的重要意义在于，由于许多常见的函数都可以用多项式逼近（幂级数展开），如常用的三角函数、对数函数都可以转换为多项式。借助差分思想，这些函数值的求解可以进一步转换为重复的加法。这样一来，绝大部分数学运算就都可以交给机器了。

差分的思想或许不难理解，但是将这一思想转化为机械，则是有一定的困难的。幸运的事，巴贝奇凭借其智慧构造了完美的设计图，但不幸的是，因为机械制造技术的限制，大量精密零件制造困难，加上巴贝奇不停地边制造边修改设计，从 1822 到 1832 年的十年间，巴贝奇只能拿出完成品的 1/7——一台支持 6 位数、2 次差分的小模型（设计稿为 20 位数、6 次差分）来展示。巴贝奇不断延后完成期限的严重超支（英国政府在 1842 年的最后清算发现整个计划一共让国库支出了￡17,500）、制作过程不断修改设计、时常与总工程师克里门发生冲突等诸多原因，让完整的差分机一号一直未能完成，一万两千多个还没用到的精密零件后来都被熔解报废。

0.3 你的程序是如何运行的

Part1 逻辑与二进制基础

Chapter01 计算机设计基础——二进制

Chapter02 基于二进制的信息存储与表示

Chapter03 基于二进制的指令设计

Chapter04 二进制硬件设计基础——时序逻辑电路

Chapter05 二进制硬件设计基础

Part2 初识冯诺依曼架构

Chapter06 初识冯诺依曼架构

Chapter07 数据通路基础设计——单周期 CPU

Chapter08 权衡风险与效率——流水线 CPU 设计

8.1 基本概念与设计

8.2 数据冒险

8.3 结构冒险

8.4 扩展流水线与多周期 CPU 设计

Chapter09 存储器层次设计

Chapter10 中断与异常

Part3 在系统上运行程序

Chapter11 初识操作系统——从一个例子开始

Chapter12 进程管理

Chapter13 内存管理

Chapter14 完整的视角：程序的装载

Part4 系统与设备的连接

Chapter15 外部存储设备

Chapter16 文件系统

16.1 文件系统接口

16.2 文件系统实现——FAT 文件系统

16.3 文件系统实现——Unix 文件系统

Chapter17 输入输出设备管理

Chapter18 计算机系统与网络

Part5 计算机系统架构的进一步优化

恭喜你进入 Part5 的学习，这表明你已经通过前四个 Part 的学习，构建出了一个功能基本完善的计算机系统。而从这一部分开始，我们希望在功能完整的基础上实现性能优化以及安全加固，这两个主题分别会在 Part5 和 Part6 中讨论。

Chapter19 更大、更快的存储层次设计

Chapter20 指令级并行技术

这一节内容相对较为基础，或许写得有些冗长，但是是融入了初次接触体系结构优化必要的思想。

20.1 ILP 基本概念与简单认识

ILP 基本概念

在本章引言中，我们已经提到 ILP 实际上是一种利用指令间潜在并行性进行优化的技术。最简单的例子便是流水线技术，它将指令的执行分为较短的几个阶段，不同的指令在同一时刻可以处于不同的执行阶段，由此实现了指令级并行。

需要注意的一点是，在本节中我们不再默认 CPU 执行是按照之前所学的五阶段顺序流水线，而是希望我们的 CPU 能够并行执行所有指令，这对于理解关于本节中依赖于冒险的概念十分重要。

基本块（Basic Block）

请阅读以下代码：

for (int i =0; i <= 999; i++)
    x[i] = x[i] + y[i];

相信你能够十分轻松地将这一段代码转化为 RISC-V 汇编代码。让你的流水线 CPU 开始执行这些代码，你将会无助地发现，无需几条指令，你的代码便会陷入控制冒险中。这显然不是我们希望看到的，但是很遗憾，对于一般的 RISC 程序，平均需要分支预测的指令比例通常在 15% 到 25% 之间，也就是说，平均约 4-7 条指令便会遭遇一次控制冒险，这并不是一个好消息。为了更好地描述这一问题，我们引入一个新的概念称为基本块。程序中的基本块只有一个入口和一个出口，入口就是其中的第—条语句，出口就是其中的最后一条语句。对一个基本块来说，执行时只从其入口进入，从其出口退出。具体而言：

只有一个入口，表示程序中不会有其它任何地方能通过跳转类指令进入到此基本块中；
只有一个出口，表示程序只有最后一条指令能导致进入到其它基本块去执行。

所以，基本块的一个典型特点是：只要基本块中第一条指令被执行了，那么基本块内所有执行都会按照顺序仅执行一次。有了基本块的定义后，前述问题可被描述为五个字：基本块太小。并且由此控制冒险严重。不仅如此，基本块中的指令间数据冒险也常常十分严重，因此严重影响ILP所需的指令间潜在并行性。为了优化这一问题，我们不难想到以下三种途径：

为了降低控制冒险的损失，我们可以使用高级的分支预测技术；
面对冲突严重的情况，我们可以通过硬件动态调度进一步挖掘并行性；
同一基本块内冲突严重，我们可以通过静态调度，使得我们可以在不同的基本块的指令间实现ILP。

1 中涉及的内容在 Chapter08 中已经介绍，在 20.4 中我们会有更多的拓展。对于 2 和 3，我们也将在之后的章节中详细讲解。

事实上，基本块这一概念不仅在体系结构中会被不断强调，在编译原理、程序分析等领域也是很基本的概念，此处不再展开，只表明其重要性。

依赖（dependence）与冒险（hazard）

在之前的学习以及本节前述内容中我们知道，指令级并行的瓶颈主要在于两点：

前后指令使用了相同的寄存器，使得指令之间存在数据依赖或名字依赖关系；
存在大量跳转指令，使得我们必须执行完跳转指令后才能确定接下来执行的指令，因此指令间还存在控制依赖。这一方面跳转指令会拖慢流水线执行效率，还有分支预测错误的可能，另一方面还会使得基本块太小，使得后文介绍的动态调度的空间非常有限。

当然根据我们在流水线一章中学习的内容，结构冒险也是潜在的瓶颈之一，但在以上两个问题严重的情况下，结构冒险的问题便不再突出，毕竟同一时刻能同时执行的指令十分有限。突破上述瓶颈的方案将会在后续章节讲解，这一两小节将为后文的分析引入一些基本概念，由此我们可以认识到，怎样的指令之间并行性会受限。

数据依赖（data dependence）

我们首先来看这样一段代码，这段代码的功能是将内存地址从 0(x1) 开始到 0(x2) 结束的每个 64 位浮点数都加上 f2 寄存器中存储的值：

Loop: 
    fld    f0, 0(x1)      // 将内存中 64 位浮点数取入 f0 寄存器
    fadd.d f4, f0, f2     // 将取入的数值加上 f2 中的数值
    fsd    f4, 0(x1)      // 存入修改后的数值
    addi   x1, x1, -8     // 读写内存的地址-8
    bne    x1, x2, Loop   // 直到 x1 = x2 不再继续

学过流水线数据冒险的我们我们不难发现，假如上述代码在简单的顺序执行流水线 CPU 上运行，

fld    f0, 0(x1)
fadd.d f4, f0, f2

这一代码片段中存在一个关于寄存器 f0 的数据冒险——因为加法指令的源操作数中用到了上一条指令的目的寄存器，于是这两条指令间便有了数据流动，即 fld 指令得到的结果通过 f0 寄存器流动到 fadd.d 指令。由此我们便引入第一种指令依赖关系——数据依赖。我们称指令 \(j\) 数据依赖于指令 \(i\) （我们称指令 \(j\) 为依赖方，指令 \(i\) 为被依赖方），如果

指令 \(j\) 需要指令 \(i\) 产生的结果作为其源操作数；
指令 \(j\) 数据依赖于指令 \(k\) ，指令 \(k\) 数据依赖于指令 \(i\) 。

事实上我们已经十分熟悉上面这种递归式的定义，1 中的描述说明了数据依赖产生的 base case，2 中的描述表明数据依赖可以形成一个“数据依赖链”，这个链条的长度甚至可以贯穿整个程序。

从数据流动的角度来看上述定义也是很清晰的，当指令 \(i\) 有数据流动到指令 \(k\) ，指令 \(k\) 又有数据流动到指令 \(j\) 时，我们可以将数据流动类比为河流，这种流动具有传递性，因此只要在同一数据依赖链上，两条指令间便有数据依赖关系。

定义数据依赖后有一个很显然的意义，即存在数据依赖的两条指令之间必须（即使两条指令在数据依赖链条中距离较远也必须如此，可以思考其中原因）依照源程序规定的执行顺序执行，否则无法确保依赖方源操作数的准确性，因此我们的动态调度、静态调度技术需要检测出这种依赖，并保证顺序执行。

还有一点需要强调的是，我们在定义的第一条中并没有限制数据依赖必须是使用了相同寄存器，实际上访问同样的内存地址也是符合定义的。但是这增大了检测依赖的难度，因为同一个内存地址可以有不同表达方式，例如可以表示为 0(x1)，也可以表示为 -12(x2)，这便增大了检测难度。在后续章节中我们会详细讲解现在的技术如何解决这一较为复杂的问题。

名字依赖（name dependence）

我们继续阅读上述代码，可以观察到以下两个代码块：

代码块 1：

fadd.d f4, f0, f2
fsd    f4, 0(x1)

代码块 2：

fsd    f4, 0(x1)
addi   x1, x1, -8

在代码块 1 中，f4 寄存器同时是两条指令的目的寄存器，在代码块 2 中，x1 寄存器在作为第一条指令的源操作数的同时是第二条指令的目的寄存器。像这样两条指令都使用了相同的寄存器或内存地址，但两条指令间没有数据流动的依赖，称为名字依赖。这里的名字实际上就是寄存器或是内存地址的另称。

事实上，在两个代码块中我们已经将名字依赖分为更具体的两种类型：

假定在一个程序中，指令 \(i\) 出现在指令 \(j\) 之前，则有以下两种名字依赖类型：

**反依赖（antidependence）**指指令 \(j\) 写入了指令 \(i\) 源操作数所在的寄存器或内存地址；
**输出依赖（output dependence）**指指令 \(i\) 和指令 \(j\) 写入了同一寄存器或内存地址。

显然，代码块 1 中出现了输出依赖，代码块 2 中出现了反依赖。学过顺序执行流水线的我们或许会疑惑，因为名字依赖不存在指令间数据流动，因此并不会引起流水线暂停或引发前递。但是为什么我们仍然需要考察这两种依赖呢？我们回顾 20.1 节开头所提及的，我们现在希望所有的指令都并行执行，那么很有可能指令 \(i\) 是一条需要较多周期执行的指令（如乘除法），指令 \(j\) 则需要较少周期即可（如加减法），假如此时存在输出依赖，那么很可能指令 \(i\) 写入目的寄存器/内存地址的时间比指令 \(j\) 晚，于是便会导致目的寄存器/内存地址的值与期望不一致。

对于反依赖，我们描述一种可能的情形，指令 \(i\) 可能因为与之前的指令存在结构冒险或数据冒险被迫暂停，而此时指令 \(j\) 直接开始执行，就有可能导致指令 \(i\) 读入被指令 \(j\) 改写后的数据，发生错误。

当然，细心的你可能会发现，我们先前并没有对两条指令源操作数中使用同一寄存器/内存地址定义依赖关系，因为这种情况无论顺序或乱序执行都不会出现上述冲突情况。

但是，名字依赖实际上都可以通过重命名的方式消除，例如我们将代码块1改为：

fadd.d f5, f0, f2
fsd    f4, 0(x1)

即我们只需在编译时刻将 fadd.d 的目的寄存器 f4 改为其他未使用的寄存器（如 f5）即可避免名字依赖的出现。当然修改 fsd 的目的寄存器也是可行的，这两种修改都需要检查其他与 f4、f5 相关的指令是否受到影响，当然实际上好的编译器会帮我们做好这些事情，于是名字依赖便可以在寄存充足的情况下被消除。

数据冒险（data hazard）

大家不难发现，我们在前文中多次提及数据依赖与数据冒险这两个词，我们十分有必要首先说明这两个词的区别，以免产生混淆，同时分析二者的联系：

数据依赖是程序本身的性质，当我们看见一个程序，便可以根据上一节中给出的定义判断存在什么数据依赖。而数据冒险是指两条指令位置足够靠近，使得两条指令并行会导致数据依赖中的寄存器/内存地址访问时机不符合预期，这是与流水线的执行策略有关的，例如采用之前学习的五阶段顺序执行流水线进行调度，输入程序可以存在名字依赖，但不会因此产生流水线数据冒险；
由1可以看出，数据依赖是产生数据冒险的原因，因此我们的优化方向一方面可以减少数据依赖的出现，相关技术（重命名）在上一节中已有初步介绍，另一方面则是在数据依赖存在的情况下通过调度技术修改流水线执行策略，尽可能减少数据冒险的出现，我们将在之后章节讲解此类技术。

我们可以根据前文中数据依赖的类型对数据冒险同样进行分类，考虑依次出现的两条指令 \(i\) 和 \(j\) ：

**RAW（read after write，写后读）**出现在存在数据依赖时，指令 \(i\) 还未写入目的寄存器/内存地址时指令 \(j\) 就读取了存在依赖的值，这种情况会导致指令 \(j\) 读取了错误的数据，可以通过前递（forwarding）或暂停（stall）解决或避免；
**WAW（write after write，写后写）**出现在存在输出依赖时，两条指令写回目的寄存器/内存地址的顺序发生了变化从而导致错误，可能的情形已在上一节提及，并且这可以直接通过重命名的方式将输出依赖解除，从而解除这一数据冒险；
**WAR（write after read，读后写）**出现在存在反依赖时，指令 \(j\) 写回与指令 \(i\) 间有依赖的寄存器/内存地址比指令 \(i\) 读入的时间早，则指令 \(i\) 读入了被修改过的数据，产生了错误。产生这一情形的原因已在上一节提及，并且这可以直接通过重命名的方式将输出依赖解除，从而解除这一数据冒险。

注意，RAR（read after read，读后读）没有对应的数据依赖且不会产生冒险，因此不构成一种数据冒险类型，理由已在之前说明。可以看到，在描述数据冒险时我们的定义描述的是执行错误的后果，这与数据依赖基于程序中指令本就存在的依赖关系的定义是有很大区别的。

控制依赖（control dependence）与分支冒险（branch hazard）

TODO: 图 20-1. 依赖与冒险的总结图

在这一节的最后，我们来完成一个简单的练习以巩固所学的知识：

练习 20.1.1

阅读以下汇编代码并回答问题，假定代码将运行在无前递（forwarding）机制的顺序执行流水线 CPU 上，跳转指令在 ID 阶段判断执行，每条指令的理想执行时间均为 1 个流水线周期：

    ld   t0, -8(x1)
    addi t1, x0, 0
    beqz t0, L2
L1:
    ld   t2, 0(x1)
    add  t1, t1, t2
    sd   t1, 0(x1)
    addi x1, x1, 8
    addi t0, t0, -1
    bnez t0, L1
L2:
    ...

请描述上述代码的功能，并写出上述代码中所有的基本块；
请写出上述代码中所有出现的数据依赖与数据冒险类型，并计算执行上述代码所需的最小周期数；
请分析 2 中数据依赖/数据冒险能否解决，并根据你的解决方法，计算出解决数据冒险后执行上述代码所需的最小周期数。